Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Mar;31(2):191-206.
doi: 10.1080/10543406.2020.1814795. Epub 2020 Sep 24.

Relative efficiency of equal versus unequal cluster sizes in cluster randomized trials with a small number of clusters

Jingxia Liu  1   2 , Chengjie Xiong  2 , Lei Liu  2 , Guoqiao Wang  2 , Luo Jingqin  1   2 , Feng Gao  1   2 , Ling Chen  2 , Yan Li  2
Affiliations

Relative efficiency of equal versus unequal cluster sizes in cluster randomized trials with a small number of clusters

Jingxia Liu et al. J Biopharm Stat. 2021 Mar.

Abstract

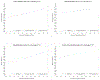
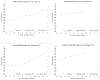
To calculate sample sizes in cluster randomized trials (CRTs), the cluster sizes are usually assumed to be identical across all clusters for simplicity. However, equal cluster sizes are not guaranteed in practice, especially when the number of clusters is limited. Therefore, it is important to understand the relative efficiency (RE) of equal versus unequal cluster sizes when designing CRTs with a limited number of clusters. In this paper, we are interested in the RE of two bias-corrected sandwich estimators of the treatment effect in the Generalized Estimating Equation (GEE) models for CRTs with a small number of clusters. Specifically, we derive the RE of two bias-corrected sandwich estimators for binary, continuous, or count data in CRTs under the assumption of an exchangeable working correlation structure. We consider different scenarios of cluster size distributions and investigate RE performance through simulation studies. We conclude that the number of clusters could be increased by as much as 42% to compensate for efficiency loss due to unequal cluster sizes. Finally, we propose an algorithm of increasing the number of clusters when the coefficient of variation of cluster sizes is known and unknown.

Keywords: Bias-corrected sandwich estimator; cluster randomized trial (CRT); generalized estimating equation (GEE); intracluster correlation coefficient (ICC); relative efficiency (RE).

PubMed Disclaimer

Conflict of interest statement

Conflict of Interest

The authors have declared no conflict of interest

Figures

Figure 1
Figure 1
Relative efficiency of the treatment effect for five distributions with m = 24, n = 5 and R = 5.
Figure 2
Figure 2
Relative efficiency of the treatment effect for five distributions with m = 24, n = 5 and R = 5 × 1.2.
Figure 3
Figure 3
Relative efficiency of the treatment effect for five distributions with m = 24, n = 5 and R = 5 × 1.6.
Figure 4
Figure 4
Relative efficiency of the treatment effect for five distributions with m = 24, n = 5 and R = 5 × 1.8.
Figure 1
Figure 1
Relative efficiency of the treatment effect for five distributions with m = 12, n = 5 and R = 5.
Figure 2
Figure 2
Relative efficiency of the treatment effect for five distributions with m = 12, n = 5 and R = 5 × 1.2.
Figure 3
Figure 3
Relative efficiency of the treatment effect for five distributions with m = 12, n = 5 and R = 5 × 1.6.
Figure 4
Figure 4
Relative efficiency of the treatment effect for five distributions with m = 12, n = 5 and R = 5 × 1.8.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Amatya A, Bhaumik D and Gibbons R (2013). Sample size determination for clustered count data. Statistics in Medicine 32:4162–4179. - PMC - PubMed
    1. Austin P (2007). A comparison of the statistical power of different methods for the analysis of cluster randomization trials with binary outcomes. Statistics in Medicine 26:3550–3565. - PubMed
    1. Candel MJJM and Van Breukelen GJP (2010). Sample size adjustments for varying cluster sizes in cluster randomized trials with binary outcomes analyzed with second-order PQL mixed logistic regression. Statistics in Medicine 29(14):1488–1501. - PubMed
    1. Candel MJJM, Van Breukelen GJP, Kotova L and Berger MPF (2008). Optimality of Equal vs. Unequal Cluster Sizes in Multilevel Intervention Studies: A Monte Carlo Study for Small Sample Sizes. Communications in Statistics - Simulation and Computation 37(1):222–239.
    1. Donner A, Birkett N and Buck C (1981). Randomization by cluster-sample size requirements and analysis. American Journal of Epidemiology 114:906–914. - PubMed

Publication types