Design of a nonlinear model for the propagation of COVID-19 and its efficient nonstandard computational implementation

Abstract

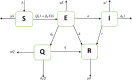
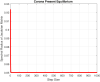
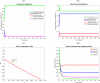
In this manuscript, we develop a mathematical model to describe the spreading of an epidemic disease in a human population. The emphasis in this work will be on the study of the propagation of the coronavirus disease (COVID-19). Various epidemiologically relevant assumptions will be imposed upon the problem, and a coupled system of first-order ordinary differential equations will be obtained. The model adopts the form of a nonlinear susceptible-exposed-infected-quarantined-recovered system, and we investigate it both analytically and numerically. Analytically, we obtain the equilibrium points in the presence and absence of the coronavirus. We also calculate the reproduction number and provide conditions that guarantee the local and global asymptotic stability of the equilibria. To that end, various tools from analysis will be employed, including Volterra-type Lyapunov functions, LaSalle's invariance principle and the Routh-Hurwitz criterion. To simulate computationally the dynamics of propagation of the disease, we propose a nonstandard finite-difference scheme to approximate the solutions of the mathematical model. A thorough analysis of the discrete model is provided in this work, including the consistency and the stability analyses, along with the capability of the discrete model to preserve the equilibria of the continuous system. Among other interesting results, our numerical simulations confirm the stability properties of the equilibrium points.

Keywords: 34D05; 65L05; 92D30; Coronavirus disease; Nonstandard numerical modeling; SEIQR model; Stability analysis.

Fig. 1

Flowchart depicting the dynamics of propagation of COVID-19 in a SEIQR model.

Fig. 2

Graph of the spectral radius of the Jacobiam matrix associated to the finite-difference scheme (3.2) at the equilibrium point C₂.The fitted and estimated parameters of Table 2 were used, and the spectral radius was obtained for various temporal step-sizes τ in [0, 1000].

Fig. 3

Solution of the system (2.1) versus time using the method (3.2), considering (a) a system free of COVID-19 and (b) a system with the presence of COVID-19. We employed the parameters of Table 1, and the initial conditions are $S_0=0.5,$$E_0=0.2,$$I_0=0.1,$$Q_0=0.1,$$R_0=0.1$ and $\tau =0.01$. (c) Dynamics of the model (2.1) when it transits from COVID-19 present to COVID-19 absent with $q_1=0.014$. (d) Dynamics of the infected individuals depending on the parameter q₁.