A bacterial size law revealed by a coarse-grained model of cell physiology

Abstract

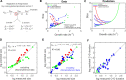
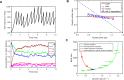
Universal observations in Biology are sometimes described as "laws". In E. coli, experimental studies performed over the past six decades have revealed major growth laws relating ribosomal mass fraction and cell size to the growth rate. Because they formalize complex emerging principles in biology, growth laws have been instrumental in shaping our understanding of bacterial physiology. Here, we discovered a novel size law that connects cell size to the inverse of the metabolic proteome mass fraction and the active fraction of ribosomes. We used a simple whole-cell coarse-grained model of cell physiology that combines the proteome allocation theory and the structural model of cell division. This integrated model captures all available experimental data connecting the cell proteome composition, ribosome activity, division size and growth rate in response to nutrient quality, antibiotic treatment and increased protein burden. Finally, a stochastic extension of the model explains non-trivial correlations observed in single cell experiments including the adder principle. This work provides a simple and robust theoretical framework for studying the fundamental principles of cell size determination in unicellular organisms.

Fig 1. A simple whole-cell coarse-grained model of bacterial growth reproduces proteome allocation and ribosome activity data.

(A) Schematic of model structure displaying model components (proteome sectors E, R, Q and X and protein precursor A) and reactions (metabolism, protein synthesis). How the three types of growth rate modulation (nutrient quality, expression of useless protein and ribosome inactivation) are modeled is also highlighted. The rate of precursor creation is proportional to the amount of metabolic enzymes E. The total protein synthesis rate is proportional to the number of active ribosomes, and the synthesis rate per ribosome (the ribosome efficiency) is dependent on the precursor concentration via a Michaelis-Menten relationship. A full description of the model is given in the Methods section. (B) Allocation of total protein synthesis capacity between proteome sectors. A fixed, condition-independent fraction f_Q is allocated to housekeeping proteins. Expression of useless protein imposes a fixed allocation f_U. The allocation to R proteins is proportional to precursor concentration, and the remainder is allocated to E proteins (assuming that f_X≪1). (C-F) Model predictions (solid lines) agree with experimental data (circles–Scott et al. 2010 [13], squares–Dai et al. 2017 [49]). Parameters were all fixed from published data (see Methods). (C) Ribosomal proteome fraction data for nutrient and chloramphenicol growth rate modulations. Colors indicate different nutrient qualities. (D) Relationship between growth rate and useless proteome fraction for forced expression of useless protein. (E-F) Ribosome efficiency ($\frac{a}{a+a_{sat}}$) and active ribosome fraction ($\frac{R_a}{R}$).

Fig 2. Integration of the structural model enables prediction of both cell composition and cell size.

(A) Simulation of model dynamics. After cell division (triggered when X number reaches X_div), cell content is partitioned equally among daughter cells and only one is followed ('mother machine' setting, Wang et al., 2010). After a transient adaptation period, concentrations of cellular components are constant, cellular growth (size increase) is exponential and division occurs at a constant size. Here, nutrient quality is such that the growth rate is 1 hr⁻¹ and there is no chloramphenicol nor useless expression. (B) Equations characterizing model steady-state together with their intuitive interpretation (see Methods for their derivation). r_a denotes the concentration of active ribosomes.

Fig 3. Regulation of division proteins by two proteome sectors quantitatively explain cell size across growth modulations.

(A) Hypothesis stating that X expression could depend on the concentration of one or two coarse-grained proteome sectors. Here we assume that X_div is invariant. (B) Empirical relationship between cell size and growth rate for three types of growth rate modulation (nutrient quality, chloramphenicol-mediated translation inhibition and expression of useless protein). Data aggregated from three studies, Basan et al. (2015), Si et al. (2017) and Taheri-Araghi et al. (2015). A scaling factor for size was applied on Si et al. and Taheri-Araghi et al. data to make the nutrient modulation data of the three studies consistent (see Fig C in S1 Text). Different branches for useless expression and chloramphenicol indicate modulations at different nutrient quality. (C) Predicted relationship between cell size and growth rate when X expression depends on both E concentration and the fraction of active ribosomes. (D-F) Log-log plots comparing model predictions with experimental data. The natural log is used. (D) Regulation of X expression by E alone can explain size data for nutrient modulation and useless expression modulation (but not chloramphenicol-mediated translation inhibition, Fig D in S1 Text). (E) Among possible regulations of X by two coarse-grained quantities, regulation by E concentration and the fraction of active ribosomes explains size data for all three types of growth rate modulations (this regulation model was used for (C)). (F) Predicted C+D durations agree with measurements by Si et al. (2017). C+D is predicted by $\mathrm{C}+\mathrm{D}=\frac{log\left[V_{div}/S_0\right]}{\alpha }$, where α is the growth rate, V_div is the model-predicted size (3C and 3E) and S₀ is a constant measured in Si et al. (2017).

Fig 4. Emergence of ‘adder’ size homeostasis and cellular individuality in the presence of reaction noise.

(A) Simulation of model dynamics with molecular noise (top: total cell size, bottom: concentrations of cellular components). At division, cellular components are randomly split between daughter cells, so the tracked daughter has a probability 1/2 of getting each mother cell component. Same parameters as in Fig 2A. The parameters X_div and $f_X^{scale}$ were chosen to obtain realistic cell-to-cell variability in size at birth and growth rate (Methods). (B) Model leads to near 'adder' size homeostasis. Average added size during one cell cycle as a function of birth cell size (via binning) is plotted. The very weak deviation towards ‘sizer’ can be explained by a residual correlation between size at birth and X count at birth due to the non-zero share of X in total size. A model variant where X is actively degraded at a constant rate and displaying a stronger deviation towards 'sizer' behavior is also shown. Other model variants exploring size homeostasis properties are discussed in Fig G in S1 Text. (C) Emergence of cellular individuality. Stochastic stimulations are performed for ten different growth conditions: seven nutrient qualities (green triangle groups), two useless expression strengths (red triangle groups) and one chloramphenicol (blue triangle groups). For each condition, cell cycles are binned by growth rate and the corresponding birth size is plotted. Continuous lines show the prediction of the deterministic model for the three growth rate modulations. Grey lines indicate experimental trends for different nutrient qualities extracted from mother machine data (Taheri-Araghi et al., 2015).