Precise/not precise (PNP): A Brunswikian model that uses judgment error distributions to identify cognitive processes

Abstract

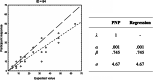
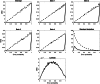
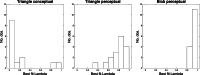
In 1956, Brunswik proposed a definition of what he called intuitive and analytic cognitive processes, not in terms of verbally specified properties, but operationally based on the observable error distributions. In the decades since, the diagnostic value of error distributions has generally been overlooked, arguably because of a long tradition to consider the error as exogenous (and irrelevant) to the process. Based on Brunswik's ideas, we develop the precise/not precise (PNP) model, using a mixture distribution to model the proportion of error-perturbed versus error-free executions of an algorithm, to determine if Brunswik's claims can be replicated and extended. In Experiment 1, we demonstrate that the PNP model recovers Brunswik's distinction between perceptual and conceptual tasks. In Experiment 2, we show that also in symbolic tasks that involve no perceptual noise, the PNP model identifies both types of processes based on the error distributions. In Experiment 3, we apply the PNP model to confirm the often-assumed "quasi-rational" nature of the rule-based processes involved in multiple-cue judgment. The results demonstrate that the PNP model reliably identifies the two cognitive processes proposed by Brunswik, and often recovers the parameters of the process more effectively than a standard regression model with homogeneous Gaussian error, suggesting that the standard Gaussian assumption incorrectly specifies the error distribution in many tasks. We discuss the untapped potentials of using error distributions to identify cognitive processes and how the PNP model relates to, and can enlighten, debates on intuition and analysis in dual-systems theories.

Keywords: Error distributions; Judgment and decision making; Mathematical models.

Fig. 1

The responses by participant ID = 24 in a willingness-to-pay task in Experiment 2 reported below plotted against the expected value, with estimated parameter values from the PNP model and a conventional regression model. A line representing the predictions of the regression model (thinner line) and a reference line x = y (thicker line) is included in the graph. The predictions by the PNP model coincide with the reference line. Note that some data points overlap

Fig. 2

The responses by participant ID = 84 in a willingness-to-pay task in Experiment 2 reported below plotted against the expected value, with estimated parameter values from the PNP model and a regression model. A line representing the predictions of both models (thinner line) and a reference line x = y (thicker line) is included in the graph. Note that some data points overlap

Fig. 3

Mean squared error for all parameters for the standard regression model (dashed line) and the PNP model (solid line) for each error probability

Fig. 4

Examples of stimuli in the condition with a conceptual triangle (a), the condition with a visual triangle (b), and the condition with the blob shape (c). In all conditions, the participants were asked to estimate the area covered by the object in square centimeters (cm²)

Fig. 5

Histograms of error distributions defined as deviations from the objective area

Fig. 6

Histograms of estimated λ parameter values for each participant in each condition

Fig. 7

Histograms of estimated λ parameter values for the dominant PNP-process model for each participant and for each condition