This is a preprint.
Quantifying heterogeneity in SARS-CoV-2 transmission during the lockdown in India
- PMID: 32995809
- PMCID: PMC7523148
- DOI: 10.1101/2020.09.10.20190017
Quantifying heterogeneity in SARS-CoV-2 transmission during the lockdown in India
Update in
-
Quantifying heterogeneity in SARS-CoV-2 transmission during the lockdown in India.Epidemics. 2021 Sep;36:100477. doi: 10.1016/j.epidem.2021.100477. Epub 2021 Jun 17. Epidemics. 2021. PMID: 34171509 Free PMC article.
Abstract
The novel SARS-CoV-2 virus shows marked heterogeneity in its transmission. Here, we used data collected from contact tracing during the lockdown in Punjab, a major state in India, to quantify this heterogeneity, and to examine implications for transmission dynamics. We found evidence of heterogeneity acting at multiple levels: in the number of potentially infectious contacts per index case, and in the per-contact risk of infection. Incorporating these findings in simple mathematical models of disease transmission reveals that these heterogeneities act in combination to strongly influence transmission dynamics. Standard approaches, such as representing heterogeneity through secondary case distributions, could be biased by neglecting these underlying interactions between heterogeneities. We discuss implications for policy, and for more efficient contact tracing in resource-constrained settings such as India. Our results highlight how contact tracing, an important public health measure, can also provide important insights into epidemic spread and control.
Figures
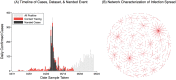

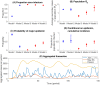

Similar articles
-
Quantifying heterogeneity in SARS-CoV-2 transmission during the lockdown in India.Epidemics. 2021 Sep;36:100477. doi: 10.1016/j.epidem.2021.100477. Epub 2021 Jun 17. Epidemics. 2021. PMID: 34171509 Free PMC article.
-
Case clustering, contact stratification, and transmission heterogeneity of SARS-CoV-2 Omicron BA.5 variants in Urumqi, China: An observational study.J Glob Health. 2023 May 19;13:06018. doi: 10.7189/jogh.13.06018. J Glob Health. 2023. PMID: 37199483 Free PMC article.
-
Social network analysis methods for exploring SARS-CoV-2 contact tracing data.BMC Med Res Methodol. 2020 Sep 17;20(1):233. doi: 10.1186/s12874-020-01119-3. BMC Med Res Methodol. 2020. PMID: 32942988 Free PMC article.
-
Heterogeneity in transmissibility and shedding SARS-CoV-2 via droplets and aerosols.Elife. 2021 Apr 16;10:e65774. doi: 10.7554/eLife.65774. Elife. 2021. PMID: 33861198 Free PMC article.
-
Digital contact tracing technologies in epidemics: a rapid review.Cochrane Database Syst Rev. 2020 Aug 18;8(8):CD013699. doi: 10.1002/14651858.CD013699. Cochrane Database Syst Rev. 2020. PMID: 33502000 Free PMC article.
References
-
- Gomes M. G. M., et al., MedRxiv p. 2020.04.27.20081893 (2020).
-
- Laxminarayan R., et al., medRxiv (2020).
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
