The turning point and end of an expanding epidemic cannot be precisely forecast

Abstract

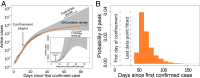
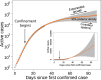
Epidemic spread is characterized by exponentially growing dynamics, which are intrinsically unpredictable. The time at which the growth in the number of infected individuals halts and starts decreasing cannot be calculated with certainty before the turning point is actually attained; neither can the end of the epidemic after the turning point. A susceptible-infected-removed (SIR) model with confinement (SCIR) illustrates how lockdown measures inhibit infection spread only above a threshold that we calculate. The existence of that threshold has major effects in predictability: A Bayesian fit to the COVID-19 pandemic in Spain shows that a slowdown in the number of newly infected individuals during the expansion phase allows one to infer neither the precise position of the maximum nor whether the measures taken will bring the propagation to the inhibition regime. There is a short horizon for reliable prediction, followed by a dispersion of the possible trajectories that grows extremely fast. The impossibility to predict in the midterm is not due to wrong or incomplete data, since it persists in error-free, synthetically produced datasets and does not necessarily improve by using larger datasets. Our study warns against precise forecasts of the evolution of epidemics based on mean-field, effective, or phenomenological models and supports that only probabilities of different outcomes can be confidently given.

Keywords: Bayesian; epidemics; forecast; predictability.

Fig. 1.

Diagram of the epidemic model along with the equations ruling the dynamics. Susceptible individuals ($S$) can enter and exit confinement ($C$) or become infected ($I$). Infected individuals can recover ($R$) or die ($D$). $N$ is the total population. Rates for each process are displayed in the figure; $q$ depends on specific measures restricting mobility and contacts, while $p$ stands for individuals that leave the confinement measures (e.g., people working at essential jobs like food supply, health care, or policing), as well as for defection. We fit $I$ to data on officially diagnosed cases, which are automatically quarantined: The underlying assumption is that the real, mostly undetected, number of infections is proportional to the diagnosed cases.

Fig. 2.

Fit to data obtained in real time for the daily number of active cases in Spain (from March 1st to March 29th) and peak forecast. (A) Despite the reasonable agreement between model and empirical observations in the growing phase, opposite predictions for the future number of active cases can be derived. The solid line represents the expression for $I\left(t\right)$ using the median parameters for each posterior in SI Appendix, Fig. S1. The vertical arrow denotes March 11th, the day when schools and universities closed. The shaded area represents the 95% predictive posterior interval: Its increasing width implies that predictability decays exponentially fast. (A, Inset) Same data and curves with linear vertical scale. SI Appendix, Figs. S6 and S7 show how this fit and its posteriors evolve as an increasing number of days is included in the fit. An animation is included as Movie S1. (B) Posterior distribution of the time to reach the peak of the epidemic, conditioned to actually having a peak (which occurs with probability 0.26). The vertical dashed lines stand for the days when the confinement began and for the date of the last data point used in the fit.

Fig. 3.

Fit to postpeak data for the daily number of active cases in Spain. (A) Fit to data up to April 18th (peak day). (B) Fit to data at three weeks postpeak (May 9th). Open symbols represent fitted empirical data, and blue dots correspond to actual measurements until May 17th. (C) Distribution of times until the number of confirmed cases falls below 1,000 for the first time. With about two cases per million inhabitants, this threshold can define the end of the epidemic. The distribution spans about three months, centered around the end of October 2020.

Fig. 4.

Data generated through direct simulation of the system described in Fig. 1 are used as input to determine posterior distributions for parameters through a Bayesian approach. Parameter values are $\beta =0.425$, $p=0.007$, $q=0.062$, and $r+\mu =0.021$ in the mitigation regime taken from the median of the posteriors in SI Appendix, Fig. S1 (all measured in ${\mathrm{d}\mathrm{a}\mathrm{y}}^{-1}$). Though the dataset is complete and noiseless, consideration of only the growing phase of the epidemic implies a remarkable uncertainty in compatible trajectories. It is worth noting that, albeit those parameters would predict that the epidemic is not controlled, variability still leaves a 3% chance that it actually is. (Inset) Same data and curves with linear vertical scale.