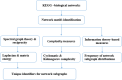
Dissecting molecular network structures using a network subgraph approach

Abstract

Biological processes are based on molecular networks, which exhibit biological functions through interactions of genetic elements or proteins. This study presents a graph-based method to characterize molecular networks by decomposing the networks into directed multigraphs: network subgraphs. Spectral graph theory, reciprocity and complexity measures were used to quantify the network subgraphs. Graph energy, reciprocity and cyclomatic complexity can optimally specify network subgraphs with some degree of degeneracy. Seventy-one molecular networks were analyzed from three network types: cancer networks, signal transduction networks, and cellular processes. Molecular networks are built from a finite number of subgraph patterns and subgraphs with large graph energies are not present, which implies a graph energy cutoff. In addition, certain subgraph patterns are absent from the three network types. Thus, the Shannon entropy of the subgraph frequency distribution is not maximal. Furthermore, frequently-observed subgraphs are irreducible graphs. These novel findings warrant further investigation and may lead to important applications. Finally, we observed that cancer-related cellular processes are enriched with subgraph-associated driver genes. Our study provides a systematic approach for dissecting biological networks and supports the conclusion that there are organizational principles underlying molecular networks.

Keywords: Biological networks; Entropy; Graph theory; Information theory; Network complexity; Network motifs; Network subgraphs.

Figure 1. The workflow of the present study.

Molecular network information were obtained from the KEGG database (August 2017). Network subgraphs were identified using PatternFinder and then network subgraphs were characterized using: graph energy, reciprocity and graph complexity. A code was developed to determine the minimal set of parameters required to label network subgraphs based on a greedy strategy. The Shannon entropy for 3-node subgraphs and 4-node subgraphs of 71 molecular networks were computed.

Figure 2. The plots of the normalized frequency of the thirteen 3-node subgraphs for (A) the cancer networks, (B) the Signal transduction networks and (C) the cellular processes.

Certain subgraphs are never present in the three molecular network types. In other words, while networks are built from a finite number of subgraph patterns, certain subgraphs associated with large graph energies are not present.

Figure 3. The plots of the normalized frequency of the 4-node subgraphs for (A) the cancer networks, (B) the signal transduction networks and (C) the cellular processes.

Only the first 120 subgraphs’ normalized frequency are shown, the rest of the subgraphs have zero normalized frequency. Eight subgraphs (id_14, id_28, id_74, id_76, id_280, id_328, id_392, and id_2184) dominate the three molecular network classes. These results indicate that molecular networks are composed of a finite number of subgraph patterns.

Figure 4. The plots of the normalized Shannon entropy for the 3-node subgraphs (black, H3R) and the 4-node subgraphs (grey, H4R), where (A) the cancer networks, (B) the signal transduction networks, and (C) the cellular processes.

The normalized frequency distributions are not uniformly distributed among the subgraph patterns. Therefore, H3R and H4R are different from zero and one.