Non-equilibrium landscape and flux reveal the stability-flexibility-energy tradeoff in working memory
- PMID: 33006962
- PMCID: PMC7531819
- DOI: 10.1371/journal.pcbi.1008209
Non-equilibrium landscape and flux reveal the stability-flexibility-energy tradeoff in working memory
Abstract
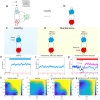
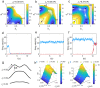
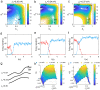
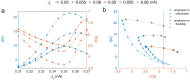
Uncovering the underlying biophysical principles of emergent collective computational abilities, such as working memory, in neural circuits is one of the most essential concerns in modern neuroscience. Working memory system is often desired to be robust against noises. Such systems can be highly flexible for adapting environmental demands. How neural circuits reconfigure themselves according to the cognitive task requirement remains unclear. Previous studies explored the robustness and the flexibility in working memory by tracing individual dynamical trajectories in a limited time scale, where the accuracy of the results depends on the volume of the collected statistical data. Inspired by thermodynamics and statistical mechanics in physical systems, we developed a non-equilibrium landscape and flux framework for studying the neural network dynamics. Applying this approach to a biophysically based working memory model, we investigated how changes in the recurrent excitation mediated by slow NMDA receptors within a selective population and mutual inhibition mediated by GABAergic interneurons between populations affect the robustness against noises. This is realized through quantifying the underlying non-equilibrium potential landscape topography and the kinetics of state switching. We found that an optimal compromise for a working memory circuit between the robustness and the flexibility can be achieved through the emergence of an intermediate state between the working memory states. An optimal combination of both increased self-excitation and inhibition can enhance the flexibility to external signals without significantly reducing the robustness to the random fluctuations. Furthermore, we found that the enhanced performance in working memory is supported by larger energy consumption. Our approach can facilitate the design of new network structure for cognitive functions with the optimal balance between performance and cost. Our work also provides a new paradigm for exploring the underlying mechanisms of many cognitive functions based on non-equilibrium physics.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
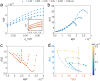
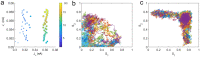
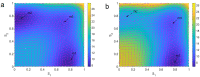
Similar articles
-
Neural mechanisms balancing accuracy and flexibility in working memory and decision tasks.NPJ Syst Biol Appl. 2025 May 7;11(1):41. doi: 10.1038/s41540-025-00520-2. NPJ Syst Biol Appl. 2025. PMID: 40335502 Free PMC article.
-
Stochastic Dynamics Underlying Cognitive Stability and Flexibility.PLoS Comput Biol. 2015 Jun 12;11(6):e1004331. doi: 10.1371/journal.pcbi.1004331. eCollection 2015 Jun. PLoS Comput Biol. 2015. PMID: 26068119 Free PMC article.
-
Working Memory and Decision-Making in a Frontoparietal Circuit Model.J Neurosci. 2017 Dec 13;37(50):12167-12186. doi: 10.1523/JNEUROSCI.0343-17.2017. Epub 2017 Nov 7. J Neurosci. 2017. PMID: 29114071 Free PMC article.
-
Working models of working memory.Curr Opin Neurobiol. 2014 Apr;25:20-4. doi: 10.1016/j.conb.2013.10.008. Epub 2013 Dec 4. Curr Opin Neurobiol. 2014. PMID: 24709596 Review.
-
From cognitive to neural models of working memory.Philos Trans R Soc Lond B Biol Sci. 2007 May 29;362(1481):761-72. doi: 10.1098/rstb.2007.2086. Philos Trans R Soc Lond B Biol Sci. 2007. PMID: 17400538 Free PMC article. Review.
Cited by
-
Quantifying the Landscape of Decision Making From Spiking Neural Networks.Front Comput Neurosci. 2021 Oct 28;15:740601. doi: 10.3389/fncom.2021.740601. eCollection 2021. Front Comput Neurosci. 2021. PMID: 34776914 Free PMC article.
-
Controlling brain dynamics: Landscape and transition path for working memory.PLoS Comput Biol. 2023 Sep 5;19(9):e1011446. doi: 10.1371/journal.pcbi.1011446. eCollection 2023 Sep. PLoS Comput Biol. 2023. PMID: 37669311 Free PMC article.
-
Neural circuit mechanisms underlying dominance traits and social competition.Biophys Rev (Melville). 2025 Jun 25;6(2):021401. doi: 10.1063/5.0221909. eCollection 2025 Jun. Biophys Rev (Melville). 2025. PMID: 40583860
-
Neural mechanisms balancing accuracy and flexibility in working memory and decision tasks.NPJ Syst Biol Appl. 2025 May 7;11(1):41. doi: 10.1038/s41540-025-00520-2. NPJ Syst Biol Appl. 2025. PMID: 40335502 Free PMC article.
-
Metastable dynamics of neural circuits and networks.Appl Phys Rev. 2022 Mar;9(1):011313. doi: 10.1063/5.0062603. Appl Phys Rev. 2022. PMID: 35284030 Free PMC article. Review.
References
-
- Deisboeck TS, Kresh JY. Complex Systems Science in Biomedicine. Springer; US; 2006. 10.1007/978-0-387-33532-2 - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

