Control of a multigroup COVID-19 model with immunity: treatment and test elimination

Abstract

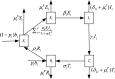
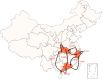
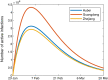
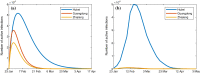
This paper introduces a multigroup COVID-19 model with immunity, in which the total population of each group is partitioned into five compartments, that is, susceptible, exposed, infective, infective in treatment and recovered compartment. If the basic reproduction number is less than or equal to one, and the infection graph is strongly connected, then the disease-free equilibrium is globally asymptotically stable and the disease dies out. However, the COVID-19 is already in a pandemic state, and the basic reproduction number is large than one. Hence, in order to make the COVID-19 die out in some groups in an area, we design some appropriate control strategies which reduce the number of exposed people and increase the number of people treated. These two methods have been proved to be the most effective methods at present. An effective algorithm is proposed to identify the groups that need to be controlled. Finally, we use the actual limited data of Hubei, Guangdong and Zhejiang provinces in China to illustrate the effectiveness of the obtained results.

Keywords: Basic reproduction number; Multigroup model; Stability.

Fig. 1

Flow diagram of the multigroup COVID-19 model

Fig. 2

The topology of cross infection among Hubei, Guangdong and Zhejiang provinces in China

Fig. 3

The number of active infections in Hubei, Guangdong and Zhejiang provinces under no control

Fig. 4

a The number of active infections in Hubei, Guangdong and Zhejiang provinces under linear control; b The actual number of active infections in Hubei, Guangdong and Zhejiang provinces

Fig. 5

The number of active infections in Hubei, Guangdong and Zhejiang provinces under finite time control