Theory of optical tweezing of dielectric microspheres in chiral host media and its applications

Abstract

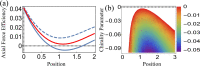
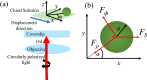
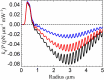
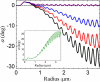
We report for the first time the theory of optical tweezers of spherical dielectric particles embedded in a chiral medium. We develop a partial-wave (Mie) expansion to calculate the optical force acting on a dielectric microsphere illuminated by a circularly-polarized, highly focused laser beam. When choosing a polarization with the same handedness of the medium, the axial trap stability is improved, thus allowing for tweezing of high-refractive-index particles. When the particle is displaced off-axis by an external force, its equilibrium position is rotated around the optical axis by the mechanical effect of an optical torque. Both the optical torque and the angle of rotation are greatly enhanced in the presence of a chiral host medium when considering radii a few times larger than the wavelength. In this range, the angle of rotation depends strongly on the microsphere radius and the chirality parameter of the host medium, opening the way for a quantitative characterization of both parameters. Measurable angles are predicted even in the case of naturally occurring chiral solutes, allowing for a novel all-optical method to locally probe the chiral response at the nanoscale.

Figure 1

(a) Normalized axial force $Q_z$ acting on a ${\text{BrO}}_2$ microsphere of radius $500\mathrm{nm}$ embedded in a chiral medium as a function of axial position (in units of the sphere radius) for different chirality parameters: $\kappa =-0.01$ (solid), $\kappa$ = 0 (red) and $\kappa =0.01$ (dashed). The incident beam is right-handed circularly polarized (helicity $\sigma =-1$). (b) Density plot of $Q_z$ versus axial position and chirality parameter. Only negative values are shown.

Figure 2

(a) Schematic representation of the optical torque on a particle trapped in a chiral medium. A right-handed ($\sigma =-1$) circularly-polarized Gaussian laser beam is focused by an oil-immersion high-NA objective into a sample filled with a chiral solution. The sample is driven laterally so as to displace the particle equilibrium position from the beam symmetry axis. (b) At equilibrium, the resulting Stokes drag force $F_S$ balances the optical force, which contains radial $F_{\rho }$ and azimuthal $F_{\varphi }$ components, the latter being responsible for the optical torque. The equilibrium position is then rotated around the beam axis by an angle $\alpha$ with respect to the direction of the Stokes force.

Figure 3

Torsion constant per unit power $k_{\varphi }/P$ as a function of the radius of a silica microsphere. The particle is embedded in a chiral solution with $\kappa =-0.001$ (blue), $-0.002$ (red) and $-0.003$ (black). The incident beam is right-handed circularly-polarized (helicity $\sigma =-1$).

Figure 4

Microsphere rotation angle $\alpha$ in degrees resulting from the optical torque on a silica microsphere (see Fig. 2) as a function of radius. The chirality parameter of the host medium is $\kappa =0$ (purple), $-0.001$ (blue), $-0.002$ (red) and $-0.003$ (black). The inset shows the case of a left-handed host medium with $\kappa =0.003$ (green) for comparison. The incident beam is right-handed circularly-polarized (helicity $\sigma =-1$). The incident beam is right-handed circularly-polarized (helicity $\sigma =-1$).

Figure 5

Microsphere rotation angle $\alpha$ in degrees versus chirality parameter $\kappa$ of the host medium for a silica microsphere of radius $a=1.5$ μm (blue) and $3.3$ μm (black). The incident beam is right-handed circularly-polarized (helicity $\sigma =-1$).

Figure 6

Numerical simulation of the effect of refraction at the planar interface between the glass coverslip and the interior of the sample chamber. As an example, we take $\kappa =-0.003.$ (a) Initial reference position of the focal plane with respect to the glass slide versus radius. The reference configuration is defined by the condition that the equilibrium position is such that the microsphere is just touching the glass slide. (b) Final focal plane position (in units of sphere radius) after displacing the objective by $d=5$ μm. (c) Equilibrium position of the microsphere (in units of sphere radius) and (d) transverse trap stiffness $k_{\rho }$ (in units of power).