Correlation dynamics of nitrogen vacancy centers located in crystal cavities

Abstract

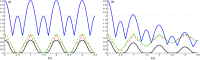
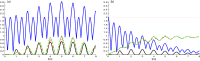
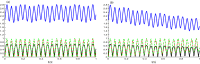
In this contribution, we investigate the bipartite non-classical correlations (NCCs) of a system formed by two nitrogen-vacancy (N-V) centers placed in two spatially separated single-mode nanocavities inside a planar photonic crystal (PC). The physical system is mathematically modeled by time-dependent Schrödinger equation and analytically solved. The bipartite correlations of the two N-V centers and the two-mode cavity have been analyzed by skew information, log-negativity, and Bell function quantifiers. We explore the effects of the coupling strength between the N-V-centers and the cavity fields as well as the cavity-cavity hopping constant and the decay rate on the generated correlation dynamics. Under some specific parameter values, a large amount of quantum correlations is obtained. This shows the possibility to control the dynamics of the correlations for the NV-centers and the cavity fields.

Figure 1

Time evolution of L(t) (dashed plots), U(t) (dashed dotted plots), M(t) (upper solid plots) and N(t) (solid plots) for large coupling case $J=0.1\tilde{g}$ with different decay rate $\chi =0.0$ in (a) and $\chi =0.1\tilde{g}$ in (b), where the NVD are prepared initially in uncorrelated state, $|\mathrm{\Psi }(0)⟩=|1_1{0}_2{g}_1{g}_2⟩$.

Figure 2

As Fig. 1 but for, the competition case $J=\tilde{g}$.

Figure 3

As Fig. 1 but for the case of the nancavities hopping coupling J greater than the N-V centers strength coupling $\tilde{g}$, where $J=10\tilde{g}$.

Figure 4

Time evolution of L(t) (dashed plots), U(t) (dashed dotted plots), M(t) (upper solid plots) and N(t) (solid plots) for large coupling case $J=0.1\tilde{g}$ with different decay rate $\chi =0.0$ in (a) and $\chi =0.1\tilde{g}$ in (b), where the NVD are prepared initially in correlated state, $|\mathrm{\Psi }(0)⟩=\frac{1}{\sqrt{2}}[|e_1{g}_2⟩+|g_1{e}_2⟩]|0_1{0}_2⟩$.

Figure 5

As Fig. 4 but for $J=\tilde{g}$.

Figure 6

Time evolution of L(t) (dashed plots), U(t) (dashed dotted plots), M(t) (upper solid plots) and N(t) (solid plots) for ${\widehat{\rho }}_{\mathit{Cav}}(t)$ and large coupling case $J=0.1\tilde{g}$ with different decay rate $\chi =0.0$ in (a) and $\chi =0.1\tilde{g}$ in (b).

Figure 7

As Fig. 6 but for the competition case $J=\tilde{g}$.

Figure 8

As Fig. 6 but for the case of the hopping coupling between the cavities grater than the coupling strength between the N-V centers, where $J=10\tilde{g}$.