Heterogeneous mass distribution of the rubble-pile asteroid (101955) Bennu

D J Scheeres¹, A S French², P Tricarico³, S R Chesley⁴, Y Takahashi⁴, D Farnocchia⁴, J W McMahon², D N Brack², A B Davis², R-L Ballouz⁵, E R Jawin⁶, B Rozitis⁷, J P Emery⁸, A J Ryan⁵, R S Park⁴, B P Rush⁴, N Mastrodemos⁴, B M Kennedy⁴, J Bellerose⁴, D P Lubey⁴, D Velez⁴, A T Vaughan⁴, J M Leonard⁹, J Geeraert⁹, B Page⁹, P Antreasian⁹, E Mazarico¹⁰, K Getzandanner¹⁰, D Rowlands¹⁰, M C Moreau¹⁰, J Small¹¹, D E Highsmith¹¹, S Goossens^{10

12}, E E Palmer³, J R Weirich³, R W Gaskell³, O S Barnouin¹³, M G Daly¹⁴, J A Seabrook¹⁴, M M Al Asad¹⁵, L C Philpott¹⁵, C L Johnson^{3

15}, C M Hartzell¹⁶, V E Hamilton¹⁷, P Michel¹⁸, K J Walsh¹⁷, M C Nolan⁵, D S Lauretta⁵

Affiliations

¹ Smead Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO, USA. scheeres@colorado.edu.
² Smead Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO, USA.
³ Planetary Science Institute, Tucson, AZ, USA.
⁴ Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, USA.
⁵ Lunar and Planetary Laboratory, University of Arizona, Tucson, AZ, USA.
⁶ Smithsonian Institution National Museum of Natural History, Washington, DC, USA.
⁷ Planetary and Space Sciences, School of Physical Sciences, The Open University, Milton Keynes, UK.
⁸ Department of Astronomy and Planetary Sciences, Northern Arizona University, Flagstaff, AZ, USA.
⁹ KinetX Aerospace Inc., Simi Valley, CA, USA.
¹⁰ NASA Goddard Space Flight Center, Greenbelt, MD, USA.
¹¹ Aerospace Corporation, Chantilly, VA, USA.
¹² Center for Research and Exploration in Space Science and Technology, University of Maryland, Baltimore County, Baltimore, MD, USA.
¹³ The Johns Hopkins University Applied Physics Laboratory, Laurel, MD, USA.
¹⁴ The Centre for Research in Earth and Space Science, York University, Toronto, ON, Canada.
¹⁵ Department of Earth, Ocean and Atmospheric Sciences, University of British Columbia, Vancouver, Canada.
¹⁶ Department of Aerospace Engineering, University of Maryland, College Park, MD, USA.
¹⁷ Department of Space Studies, Southwest Research Institute, Boulder, CO, USA.
¹⁸ Université Côte d'Azur, Observatoire de la Côte d'Azur, CNRS, Laboratoire Lagrange, Nice, France.

PMID: 33033036
PMCID: PMC7544499
DOI: 10.1126/sciadv.abc3350

Heterogeneous mass distribution of the rubble-pile asteroid (101955) Bennu

D J Scheeres et al. Sci Adv. 2020.

. 2020 Oct 8;6(41):eabc3350.

doi: 10.1126/sciadv.abc3350. Print 2020 Oct.

Authors

Affiliations

¹ Smead Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO, USA. scheeres@colorado.edu.
² Smead Department of Aerospace Engineering Sciences, University of Colorado, Boulder, CO, USA.
³ Planetary Science Institute, Tucson, AZ, USA.
⁴ Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, USA.
⁵ Lunar and Planetary Laboratory, University of Arizona, Tucson, AZ, USA.
⁶ Smithsonian Institution National Museum of Natural History, Washington, DC, USA.
⁷ Planetary and Space Sciences, School of Physical Sciences, The Open University, Milton Keynes, UK.
⁸ Department of Astronomy and Planetary Sciences, Northern Arizona University, Flagstaff, AZ, USA.
⁹ KinetX Aerospace Inc., Simi Valley, CA, USA.
¹⁰ NASA Goddard Space Flight Center, Greenbelt, MD, USA.
¹¹ Aerospace Corporation, Chantilly, VA, USA.
¹² Center for Research and Exploration in Space Science and Technology, University of Maryland, Baltimore County, Baltimore, MD, USA.
¹³ The Johns Hopkins University Applied Physics Laboratory, Laurel, MD, USA.
¹⁴ The Centre for Research in Earth and Space Science, York University, Toronto, ON, Canada.
¹⁵ Department of Earth, Ocean and Atmospheric Sciences, University of British Columbia, Vancouver, Canada.
¹⁶ Department of Aerospace Engineering, University of Maryland, College Park, MD, USA.
¹⁷ Department of Space Studies, Southwest Research Institute, Boulder, CO, USA.
¹⁸ Université Côte d'Azur, Observatoire de la Côte d'Azur, CNRS, Laboratoire Lagrange, Nice, France.

PMID: 33033036
PMCID: PMC7544499
DOI: 10.1126/sciadv.abc3350

Abstract

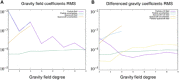
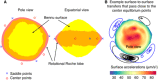
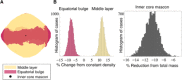
The gravity field of a small body provides insight into its internal mass distribution. We used two approaches to measure the gravity field of the rubble-pile asteroid (101955) Bennu: (i) tracking and modeling the spacecraft in orbit about the asteroid and (ii) tracking and modeling pebble-sized particles naturally ejected from Bennu's surface into sustained orbits. These approaches yield statistically consistent results up to degree and order 3, with the particle-based field being statistically significant up to degree and order 9. Comparisons with a constant-density shape model show that Bennu has a heterogeneous mass distribution. These deviations can be modeled with lower densities at Bennu's equatorial bulge and center. The lower-density equator is consistent with recent migration and redistribution of material. The lower-density center is consistent with a past period of rapid rotation, either from a previous Yarkovsky-O'Keefe-Radzievskii-Paddack cycle or arising during Bennu's accretion following the disruption of its parent body.

Copyright © 2020 The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. No claim to original U.S. Government Works. Distributed under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC).

PubMed Disclaimer

Figures

**Fig. 1. Spacecraft- and particle-based gravity fields and uncertainties as a function of degree and order.**
Absolute magnitudes (A) and differences between estimated values and the constant-density gravity field (B). Motivated by this comparison, the particle field is used for all subsequent analysis.

**Fig. 2. Surface variations due to density variations up to degree and order 4.**
(A) Difference between measured and constant-density surface accelerations shown on the shape model and in terms of surface latitude and longitude, measured in terms of percent variation (top) and microgals (bottom). (B) Geopotential slope variations using both views.

**Fig. 3. The energetics and dynamics associated with close motion about Bennu.**
(A) Bennu’s rotational Roche lobe, along with locations and type of its co-orbital equilibrium points. (B) Select trajectories lofted from the surface that fly close to the center manifolds.

**Fig. 4. Surface slopes on Bennu.**
(A) Slopes mapped to the Bennu surface (color scale) showing the intersection of the rotational Roche lobe (the fence; black lines) with the surface. (B) Longitudinally averaged slopes (top) and radius (bottom) as a function of Bennu latitude. The numbers shown in the plots are the average values within and outside of the Roche lobe.

**Fig. 5. Randomly generated feasible density distributions computed using the GGI technique.**
Images show slices through the *y-z* plane. Those marked with a yellow star have similar characteristics to the analytical model of an underdense center and equatorial bulge, those with a blue star do not share the geometric characteristics, and those with a piebald star have some of the features. These represent a sampling of possible density distributions that are consistent with the shape and gravity field but are not individually statistically significant.

**Fig. 6. Three-component density model and fits, accounting for the gravity field covariance.**
Constant-density components (A) and candidate density and mass distributions (B) to fit the hypothesized variation, computed accounting for gravity field coefficients, and their associated covariance.

See this image and copyright information in PMC

References

1. Russell C. T., Raymond C. A., Coradini A., McSween H. Y., Zuber M. T., Nathues A., De Sanctis M. C., Jaumann R., Konopliv A. S., Preusker F., Asmar S. W., Park R. S., Gaskell R., Keller H. U., Mottola S., Roatsch T., Scully J. E. C., Smith D. E., Tricarico P., Toplis M. J., Christensen U. R., Feldman W. C., Lawrence D. J., McCoy T. J., Prettyman T. H., Reedy R. C., Sykes M. E., Titus T. N., Dawn at Vesta: Testing the protoplanetary paradigm. Science 336, 684–686 (2012). - PubMed
1. Ermakov A. I., Zuber M. T., Smith D. E., Raymond C. A., Balmino G., Fu R. R., Ivanov B. A., Constraints on Vesta’s interior structure using gravity and shape models from the Dawn mission. Icarus 240, 146–160 (2014).
1. Park R. S., Konopliv A. S., Bills B. G., Rambaux N., Castillo-Rogez J. C., Raymond C. A., Vaughan A. T., Ermakov A. I., Zuber M. T., Fu R. R., Toplis M. J., Russell C. T., Nathues A., Preusker F., A partially differentiated interior for (1) Ceres deduced from its gravity field and shape. Nature 537, 515–517 (2016). - PubMed
1. Ermakov A. I., Fu R. R., Castillo-Rogez J. C., Raymond C. A., Park R. S., Preusker F., Russell C. T., Smith D. E., Zuber M. T., Constraints on Ceres’ internal structure and evolution from its shape and gravity measured by the Dawn spacecraft. J. Geophys. Res. Planets 122, 2267–2293 (2017).
1. Konopliv A. S., Park R. S., Vaughan A. T., Bills B. G., Asmar S. W., Ermakov A. I., Rambaux N., Raymond C. A., Castillo-Rogez J. C., Russell C. T., Smith D. E., Zuber M. T., The Ceres gravity field, spin pole, rotation period and orbit from the Dawn radiometric tracking and optical data. Icarus 299, 411–429 (2018).

LinkOut - more resources

Full Text Sources
Miscellaneous
- NCI CPTAC Assay Portal

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Heterogeneous mass distribution of the rubble-pile asteroid (101955) Bennu

Affiliations

Heterogeneous mass distribution of the rubble-pile asteroid (101955) Bennu

Authors

Affiliations

Abstract

Figures

References

LinkOut - more resources

Full Text Sources

Miscellaneous