COVID-19 pandemic and chaos theory

Abstract

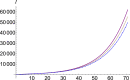
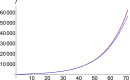
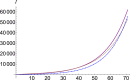
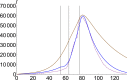
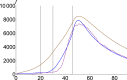
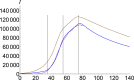
The dynamics of COVID-19 is investigated with regard to complex contributions of the omitted factors. For this purpose, we use a fractional order SEIR model which allows us to calculate the number of infections considering the chaotic contributions into susceptible, exposed, infectious and removed number of individuals. We check our model on Wuhan, China-2019 and South Korea underlying the importance of the chaotic contribution, and then we extend it to Italy and the USA. Results are of great guiding significance to promote evidence-based decisions and policy.

Keywords: Bernoulli polynomials; Block-pulse; Caputo derivative; Epidemic models.

Fig. 1

Infected number $I$, $c=\lambda =1$ (purple, continuous), $c=\lambda =0.99$ (brown, dotted) and $c=\lambda =0.98$ (blue, dot-dashed).

Fig. 2

Infected number $I$, $a=\theta =1$ (purple, continuous), $a=\theta =0.1$ (brown, dotted) and $a=\theta =1.8$ (blue, dot-dashed).

Fig. 3

Infected number $I$, $b=\eta =1$ (purple, continuous), $b=\eta =0.9$ (brown, dotted) and $b=\eta =1.3$ (blue, dot-dashed).

Fig. 4

Infected number $I$, $b=\eta =1$ (purple, continuous), $b=\eta =0.9$ (brown, dotted) and $b=\eta =0.5$ (blue, dot-dashed), for $R_0=1.8$.

Fig. 5

Infected number $I$ for China. Data is plotted with purple, SEIR solution with brown, and the fractional model $c_1={\lambda }_1=0.9$, $c_2={\lambda }_2=1.3$, $c_3={\lambda }_3=1.35$, $c_4={\lambda }_4=1.15$ and $b_4={\eta }_4=1.3$ with blue.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6

Infected number $I$ for South Korea. Data is plotted with purple, SEIR solution with brown, and the fractional model $c_1={\lambda }_1=0.7$, $c_2={\lambda }_2=1.2$, $c_3={\lambda }_3=1.35$, $c_4={\lambda }_4=1.05$ and $b_4={\eta }_4=1.2$ with blue.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7

Infected number $I$ for Italy. Data is plotted with purple, SEIR solution with brown, and the fractional model $c_1={\lambda }_1=0.9$, $c_2={\lambda }_2=1.25$, $c_3={\lambda }_3=1.3$, $c_4={\lambda }_4=1.1$ and $b_4={\eta }_4=1.25$ with blue.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 8

Infected number $I$ for USA. Data is plotted with purple, SEIR solution with brown, and the fractional model $c_1={\lambda }_1=0.9$, $c_2={\lambda }_2=1.15$, $c_3={\lambda }_3=1.2$, $c_4={\lambda }_4=1$ and $b_4={\eta }_4=1.15$ with blue.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)