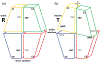
Characterizing pathological imperfections in macromolecular crystals: lattice disorders and modulations
- PMID: 33041501
- PMCID: PMC7546027
- DOI: 10.1080/0889311x.2019.1692341
Characterizing pathological imperfections in macromolecular crystals: lattice disorders and modulations
Figures











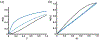
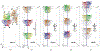




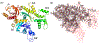



References
-
- Helliwell JR. Macromolecular crystal twinning, lattice disorders and multiple crystals. Crystallogr Rev. 2008;14(3):189–250.
-
- Parsons S Introduction to twinning. Acta Cryst. 2003;D59:1995–2003. - PubMed
-
- Yeates TO. Detecting and overcoming crystal twinning. Methods Enzymol. 1997;276:344–358. - PubMed
-
- Yeates TO, Fam BC. Protein crystals and their evil twins. Structure. 1999;7(2):R25–9. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
