Dynamical persistence in high-diversity resource-consumer communities

Abstract

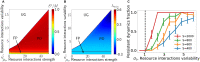
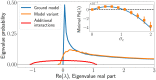
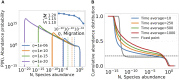
We show how highly-diverse ecological communities may display persistent abundance fluctuations, when interacting through resource competition and subjected to migration from a species pool. These fluctuations appear, robustly and predictably, in certain regimes of parameter space. Their origin is closely tied to the ratio of realized species diversity to the number of resources. This ratio is set by competition, through the balance between species being pushed out and invading. When this ratio is smaller than one, dynamics will reach stable equilibria. When this ratio is larger than one, the competitive exclusion principle dictates that fixed-points are either unstable or marginally stable. If they are unstable, the system is repelled from fixed points, and abundances forever fluctuate. While marginally-stable fixed points are in principle allowed and predicted by some models, they become structurally unstable at high diversity. This means that even small changes to the model, such as non-linearities in how resources combine to generate species' growth, will result in persistent abundance fluctuations.

Fig 1. Overview of argument.

(A) The spectrum of response to perturbations. Fixed points encountered by a high-diversity resource-competition community may be unstable. (B) Marginally-stable fixed points (or nearly marginal ones) that appear in certain models, are characterized by a non-negative spectrum. The community can relax to a fixed point, but the stability of such fixed points is sensitive to modeling assumptions, including additional interactions of other types, or how growth rates depend on resource availability. (C) In the presence of migration an instability in the fixed point creates persistent abundance fluctuations, in which species are pushed out due to the instability, but are later able to invade again. (D) In such a case, the directions corresponding to the nearly marginal eigenvectors become “soft” directions, showing large fluctuations. For clarity, in (B,C) 30 representative species are plotted.

Fig 2. The model exhibits three phases, i.e. regions with qualitatively distinct behavior.

In one, the system converges to a stable fixed point (FP), in another fixed points of the system are unstable yielding persistent dynamics (PD). In the third phase, unbounded growth (UG), species abundances grow without bound. ω is adjusted in order to maintain constant perturbation strength of 0.05. (A) Color map of the ratio S*/M, indicating how close the system is to competitive exclusion S*/M = 1, assuming an equilibrium reached. In the PD phase the calculation of S*/M is no longer valid and S*/M > 1 may be reached (see later sections). (B) The minimal real part of eigenvalues of the interaction matrix between coexisting species, λ_min. Fixed point stability is lost at λ_min = 0, where the solid line separates the FP and PD phases. The increase in S*/M reduces the stability of the equilibria, triggering a transition to persistent dynamics. (C) Probability of reaching persistent dynamics along a vertical cross section of the diagrams in panels A and B, in simulations with different pool richness S. The transition between equilibrium and non-equilibrium outcomes becomes sharper as system size increases, and matches the theoretically predicted transition point between the phases (dashed line).

Fig 3. Spectrum of α*, the interaction matrix of persistent species, in the ground model (blue), and the variant with additional direct interactions (orange).

The perturbation spectrum is shown in red, to illustrate its size we normalize the area under the perturbation spectrum to the size of the relative perturbation strength (0.05). (Inset) Minimal eigenvalue real part of the reduced interaction matrix α*, when varying σ_c at fixed μ_c. Solid line is theoretical curve. A phase transition occurs when the minimal real part of the eigenvalues crosses λ_min = 0, from λ_min > 0 at which fixed points of the dynamical system are stable, to λ_min < 0 where all fixed points are unstable and persistent dynamics ensue. For example, here the transition happens at σ_c close to 1.

Fig 4. The transition between the equilibrium and persistent dynamics phases in a model with non-linear resource intake.

(A) As model parameters are changed (here varying σ_c) the fraction of systems exhibiting persistent dynamics varies. Communities reaching a fixed-point must satisfy S*/M < 1 due to competitive exclusion, but in the persistent dynamics regime can sustain more coexisting species, with S*/M > 1. (B) The relative perturbation strength, ρ, quantifies how much the growth-rate as a function of resource availability deviates from the weighted linear sum (see text for definition). ρ changes as model parameters are changed, and is measured in simulations. Persistent non-equilibrium dynamics already found for ρ ≳ 0.06 marked by dashed vertical line.

Fig 5. Diversity above competitive exclusion in the non-linear resource competition model, see Sec. Non-linear resource intake.

(A) Abundance distribution for different values of migration. The area to the right of the vertical lines hold exactly M species. The rest of the distribution, below the line, accounts for species above competitive exclusion. Inset: the total number of coexisting species normalized by number of resources, with values above one indicate crossing of competitive exclusion. (B) Due to the abundance fluctuations, averaging abundances over a time window pushes the distribution of abundance upwards due to fluctuations. The cumulative abundance distribution is shown, defined as $\mathcal{F}(N)=\frac{1}{S}{\displaystyle {\sum }_i{1}_{[{\overline{N}}_i>N]}}.$ The dashed line is the competitive exclusion bound, M/S. For comparison, the distribution at a fixed point is given, showing that the number of species at high abundance(N ≳ 10⁻³ does not reach this bound, and the rest of the species are at low abundances, only supported by migration.