The non-Newtonian maxwell nanofluid flow between two parallel rotating disks under the effects of magnetic field

Abstract

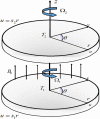
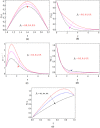
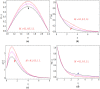
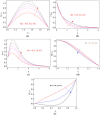
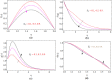
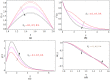
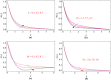
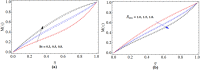
The main feature of the present numerical model is to explore the behavior of Maxwell nanoliquid moving within two horizontal rotating disks. The disks are stretchable and subjected to a magnetic field in axial direction. The time dependent characteristics of thermal conductivity have been considered to scrutinize the heat transfer phenomena. The thermophoresis and Brownian motion features of nanoliquid are studied with Buongiorno model. The lower and upper disk's rotation for both the cases, same direction as well as opposite direction of rotation is investigated. The subsequent arrangement of the three dimensional Navier Stoke's equations along with energy, mass and Maxwell equations are diminished to a dimensionless system of equations through the Von Karman's similarity framework. The comparative numerical arrangement of modeled equations is further set up by built-in numerical scheme "boundary value solver" (Bvp4c) and Runge Kutta fourth order method (RK4). The various physical constraints, such as Prandtl number, thermal conductivity, magnetic field, thermal radiation, time relaxation, Brownian motion and thermophoresis parameters and their impact are presented and discussed briefly for velocity, temperature, concentration and magnetic strength profiles. In the present analysis, some vital characteristics such as Nusselt and Sherwood numbers are considered for physical and numerical investigation. The outcomes concluded that the disk stretching action opposing the flow behavior. With the increases of magnetic field parameter [Formula: see text] the fluid velocity decreases, while improving its temperature. We show a good agreement of the present work by comparing with those published in literature.

Figure 1

Geometry of the problem.

Figure 2

${\beta }_1$ impact on axial $f\left(\eta \right)$, radial $f^{\prime }\left(\eta \right)$ and azimuthal velocity $g\left(\eta \right)$, temperature $\mathrm{\Theta }\left(\eta \right)$ and pressure profile $P\left(\eta \right)$, for $S_2$, when $S_1$ = 0.0. dashed lines for $\mathrm{\Omega }$ = 0.5 and lines for $\mathrm{\Omega }$ =  − 0.5.

Figure 3

$M$ impact on an axial $f\left(\eta \right)$, radial $f^{\prime }\left(\eta \right)$ and azimuthal velocity $g\left(\eta \right)$ and temperature profile $\mathrm{\Theta }\left(\eta \right)$, for $S_2$, when $S_1$ = 0.0. dashed lines for $\mathrm{\Omega }$ = 0.5 and lines for $\mathrm{\Omega }$ =  − 0.5.

Figure 4

$\text{Re}$ impact on axial $f\left(\eta \right)$, radial $f^{\prime }\left(\eta \right)$ and azimuthal velocity $g\left(\eta \right)$, temperature profile $\mathrm{\Theta }\left(\eta \right)$ and pressure profile $P\left(\eta \right)$, for $S_2$, when $S_1$ = 0.0. dashed lines for $\mathrm{\Omega }$ = 0.5 and lines for $\mathrm{\Omega }$ =  − 0.5.

Figure 5

$S_2$ impact on axial $f\left(\eta \right)$, radial $f^{\prime }\left(\eta \right)$ and azimuthal velocity $g\left(\eta \right)$ and temperature profile $\mathrm{\Theta }\left(\eta \right)$, for $S_2$, when $S_1$ = 0.0. dashed lines for $\mathrm{\Omega }$ = 0.5 and lines for $\mathrm{\Omega }$ =  − 0.5.

Figure 6

$S_2$ impact on axial $f\left(\eta \right)$, radial $f^{\prime }\left(\eta \right)$ and azimuthal velocity $g\left(\eta \right)$ and temperature profile $\mathrm{\Theta }\left(\eta \right)$, for $S_2$, when $S_1$ = 0.5. dashed lines for $\mathrm{\Omega }$ = 0.5 and lines for $\mathrm{\Omega }$ =  − 0.5.

Figure 7

$\epsilon$ and Pr impact on temperature profile $\mathrm{\Theta }\left(\eta \right)$, while Nt and Sc on concentration profile, for $S_2$, when $S_1$ = 0.0. dashed lines for $\mathrm{\Omega }$ = 0.5 and lines for $\mathrm{\Omega }$ =  − 0.5.

Figure 8

$\mathit{Bt}$ and $R_{\mathit{em}}$ impact on magnetic strength profile $M\left(\eta \right)$ for $S_2$, when $S_1$ = 0.0. dashed lines for $\mathrm{\Omega }$ = 0.5 and lines for $\mathrm{\Omega }$ =  − 0.5.