The Geometry of Abstraction in the Hippocampus and Prefrontal Cortex
- PMID: 33058757
- PMCID: PMC8451959
- DOI: 10.1016/j.cell.2020.09.031
The Geometry of Abstraction in the Hippocampus and Prefrontal Cortex
Abstract
The curse of dimensionality plagues models of reinforcement learning and decision making. The process of abstraction solves this by constructing variables describing features shared by different instances, reducing dimensionality and enabling generalization in novel situations. Here, we characterized neural representations in monkeys performing a task described by different hidden and explicit variables. Abstraction was defined operationally using the generalization performance of neural decoders across task conditions not used for training, which requires a particular geometry of neural representations. Neural ensembles in prefrontal cortex, hippocampus, and simulated neural networks simultaneously represented multiple variables in a geometry reflecting abstraction but that still allowed a linear classifier to decode a large number of other variables (high shattering dimensionality). Furthermore, this geometry changed in relation to task events and performance. These findings elucidate how the brain and artificial systems represent variables in an abstract format while preserving the advantages conferred by high shattering dimensionality.
Keywords: abstraction; anterior cingulate cortex; artificial neural networks; dimensionality; disentangled representations; factorized representations; hippocampus; mixed selectivity; prefrontal cortex; representational geometry.
Copyright © 2020 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of Interests The authors declare no competing interests.
Figures

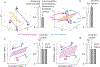

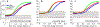

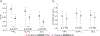

References
-
- Barto AG & Mahadevan S (2003), ‘Recent advances in hierarchical reinforcement learning’, Discrete Event Dynamic Systems 13(4), 341–379.
-
- Behrens TE, Muller TH, Whittington JC, Mark S, Baram AB, Stachenfeld KL & Kurth-Nelson Z (2018), ‘What is a cognitive map? organizing knowledge for flexible behavior’, Neuron 100(2), 490–509. - PubMed
-
- Bellman RE (1957), Dynamic Programming., Princeton University Press.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

