Faraday waves in soft elastic solids

Abstract

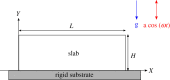
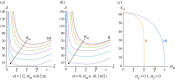
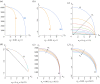
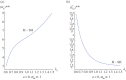
Recent experiments have observed the emergence of standing waves at the free surface of elastic bodies attached to a rigid oscillating substrate and subjected to critical values of forcing frequency and amplitude. This phenomenon, known as Faraday instability, is now well understood for viscous fluids but surprisingly eluded any theoretical explanation for soft solids. Here, we characterize Faraday waves in soft incompressible slabs using the Floquet theory to study the onset of harmonic and subharmonic resonance eigenmodes. We consider a ground state corresponding to a finite homogeneous deformation of the elastic slab. We transform the incremental boundary value problem into an algebraic eigenvalue problem characterized by the three dimensionless parameters, that characterize the interplay of gravity, capillary and elastic waves. Remarkably, we found that Faraday instability in soft solids is characterized by a harmonic resonance in the physical range of the material parameters. This seminal result is in contrast to the subharmonic resonance that is known to characterize viscous fluids, and opens the path for using Faraday waves for a precise and robust experimental method that is able to distinguish solid-like from fluid-like responses of soft matter at different scales.

Keywords: Faraday waves; Floquet theory; nonlinear elasticity; soft solid.

Figure 1.

Faraday waves in soft gels: (a) schematic of experimental set-up, (b) typical wave pattern for a gel with shear modulus μ = 19 Pa in a square container, as it depends upon driving frequency f, and (c) typical instability tongue plotting critical acceleration a against frequency f for a given mode in a circular container.

Figure 2.

Sketch of the reference configuration of the model: L is the reference length of the elastic slab and H is its reference height. It is clamped to a rigid substrate and it is subjected to its own weight and to a vertical sinusoidal oscillation with amplitude a and frequency ω. (Online version in colour.)

Figure 3.

Marginal stability curves showing the order parameter $\tilde{a}$ versus the horizontal wavenumber $\tilde{k}$ where we fix λ_x = 1, ${\alpha }_{\gamma }=0$ and α_g = 0.1. (a) α = 1/2 and ${\alpha }_{\omega }=\{0.5,1,2,2.5,3,3.1,\pi \}$; (b) α = 0 and ${\alpha }_{\omega }=\{0.3,0.6,0.9,1.3,1.5,1.56,\pi /2\}$. (c) Critical threshold ${\tilde{a}}_{\text{cr}}$ versus ${\alpha }_{\omega }$ fixing λ_x = 1, ${\alpha }_{\gamma }=0$ and α_g = 0.1: the blue line is the subharmonic case α = 1/2 (SH), while the yellow one is the harmonic resonant mode α = 0 (H). (Online version in colour.)

Figure 4.

Plot of the critical value ${\tilde{a}}_{\text{cr}}$ and the critical wavenumber ${\tilde{k}}_{\text{cr}}$ versus α_ω fixing λ_x = 1 and varying the physical quantities. (a–b) ${\alpha }_{\gamma }=0$ and α_g = 0.001, (c) α = 0, ${\alpha }_{\gamma }=0$ and α_g ∈ [1, 5] step 0.5 for graphical reasons, (d) α = 0, ${\alpha }_{\gamma }=0$ and α_g ∈ [0, 6.22] step 0.2, (e–f ) α = 0, α_g = 0.001 and ${\alpha }_{\gamma }\in [0,0.2]$ step 0.05. In (a–b), the yellow line is the harmonic solution while the blue one is the subharmonic one. (Online version in colour.)

Figure 5.

Plot of the critical values ${\tilde{a}}_{\text{cr}}$ and the critical wavenumber ${\tilde{k}}_{\text{cr}}$ versus α_ω fixing the first unstable resonant mode, i.e. α = 0 and varying λ_x ∈ [0.7, 1.4] step 0.1. (a–b) α_g = 0.001, α_γ = 0, (c–d) α_g = 0.1, ${\alpha }_{\gamma }=0$, (e–f ) α_g = 0.001, α_γ = 0.05. (Online version in colour.)

Figure 6.

Plot of the (a) critical values (α_g)^min and (b) ${({\tilde{k}}_{\text{cr}})}^{\text{min}}$ versus λ_x in the limit of ${\alpha }_{\omega }\ll 1$ fixing a = 0 and ${\alpha }_{\gamma }=0$. (Online version in colour.)