Rapid prediction of crucial hotspot interactions for icosahedral viral capsid self-assembly by energy landscape atlasing validated by mutagenesis
- PMID: 33079933
- PMCID: PMC7598928
- DOI: 10.1371/journal.pcbi.1008357
Rapid prediction of crucial hotspot interactions for icosahedral viral capsid self-assembly by energy landscape atlasing validated by mutagenesis
Abstract
Icosahedral viruses are under a micrometer in diameter, their infectious genome encapsulated by a shell assembled by a multiscale process, starting from an integer multiple of 60 viral capsid or coat protein (VP) monomers. We predict and validate inter-atomic hotspot interactions between VP monomers that are important for the assembly of 3 types of icosahedral viral capsids: Adeno Associated Virus serotype 2 (AAV2) and Minute Virus of Mice (MVM), both T = 1 single stranded DNA viruses, and Bromo Mosaic Virus (BMV), a T = 3 single stranded RNA virus. Experimental validation is by in-vitro, site-directed mutagenesis data found in literature. We combine ab-initio predictions at two scales: at the interface-scale, we predict the importance (cruciality) of an interaction for successful subassembly across each interface between symmetry-related VP monomers; and at the capsid-scale, we predict the cruciality of an interface for successful capsid assembly. At the interface-scale, we measure cruciality by changes in the capsid free-energy landscape partition function when an interaction is removed. The partition function computation uses atlases of interface subassembly landscapes, rapidly generated by a novel geometric method and curated opensource software EASAL (efficient atlasing and search of assembly landscapes). At the capsid-scale, cruciality of an interface for successful assembly of the capsid is based on combinatorial entropy. Our study goes all the way from resource-light, multiscale computational predictions of crucial hotspot inter-atomic interactions to validation using data on site-directed mutagenesis' effect on capsid assembly. By reliably and rapidly narrowing down target interactions, (no more than 1.5 hours per interface on a laptop with Intel Core i5-2500K @ 3.2 Ghz CPU and 8GB of RAM) our predictions can inform and reduce time-consuming in-vitro and in-vivo experiments, or more computationally intensive in-silico analyses.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
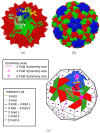




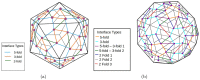
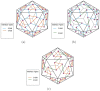
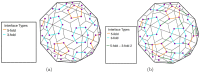




Similar articles
-
Structural and Biophysical Analysis of Adeno-Associated Virus Serotype 2 Capsid Assembly Variants.J Virol. 2023 Jul 27;97(7):e0177222. doi: 10.1128/jvi.01772-22. Epub 2023 Jun 13. J Virol. 2023. PMID: 37310260 Free PMC article.
-
Nuclear transport of trimeric assembly intermediates exerts a morphogenetic control on the icosahedral parvovirus capsid.J Mol Biol. 2006 Mar 31;357(3):1026-38. doi: 10.1016/j.jmb.2006.01.019. Epub 2006 Jan 23. J Mol Biol. 2006. PMID: 16469332
-
Atlasing of Assembly Landscapes using Distance Geometry and Graph Rigidity.J Chem Inf Model. 2020 Oct 26;60(10):4924-4957. doi: 10.1021/acs.jcim.0c00763. Epub 2020 Sep 16. J Chem Inf Model. 2020. PMID: 32786706
-
Assembly of Structurally Simple Icosahedral Viruses.Subcell Biochem. 2024;105:403-430. doi: 10.1007/978-3-031-65187-8_11. Subcell Biochem. 2024. PMID: 39738953 Review.
-
Bacteriophage HK97 capsid assembly and maturation.Adv Exp Med Biol. 2012;726:351-63. doi: 10.1007/978-1-4614-0980-9_15. Adv Exp Med Biol. 2012. PMID: 22297521 Review.
Cited by
-
Modeling Viral Capsid Assembly: A Review of Computational Strategies and Applications.Cells. 2024 Dec 17;13(24):2088. doi: 10.3390/cells13242088. Cells. 2024. PMID: 39768179 Free PMC article. Review.
-
A new discrete-geometry approach for integrative docking of proteins using chemical crosslinks.bioRxiv [Preprint]. 2025 Jan 7:2024.10.24.619977. doi: 10.1101/2024.10.24.619977. bioRxiv. 2025. Update in: J Chem Inf Model. 2025 May 12;65(9):4576-4592. doi: 10.1021/acs.jcim.4c02412. PMID: 39553940 Free PMC article. Updated. Preprint.
References
-
- Caspar DL, Klug A. Physical principles in the construction of regular viruses In: Cold Spring Harbor symposia on quantitative biology. vol. 27 Cold Spring Harbor Laboratory Press; 1962. p. 1–24. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

