Explaining anaesthetic hysteresis with effect-site equilibration
- PMID: 33081972
- PMCID: PMC7844350
- DOI: 10.1016/j.bja.2020.09.022
Explaining anaesthetic hysteresis with effect-site equilibration
Abstract
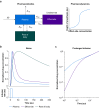
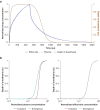
Background: Anaesthetic induction occurs at higher plasma drug concentrations than emergence in animal studies. Some studies find evidence for such anaesthetic hysteresis in humans, whereas others do not. Traditional thinking attributes hysteresis to drug equilibration between plasma and the effect site. Indeed, a key difference between human studies showing anaesthetic hysteresis and those that do not is in how effect-site equilibration was modelled. However, the effect-site is a theoretical compartment in which drug concentration cannot be measured experimentally. Thus, it is not clear whether drug equilibration models with experimentally intractable compartments are sufficiently constrained to unequivocally establish evidence for the presence or absence of anaesthetic hysteresis.
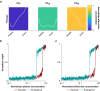
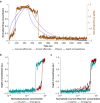
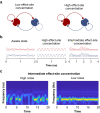
Methods: We constructed several models. One lacked hysteresis beyond effect-site equilibration. In another, neuronal dynamics contributed to hysteresis. We attempted to distinguish between these two systems using drug equilibration models.
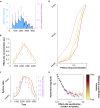
Results: Our modelling studies showed that one can always construct an effect-site equilibration model such that hysteresis collapses. So long as the concentration in the effect-site cannot be measured directly, the correct effect-site equilibration model and the one that erroneously collapses hysteresis are experimentally indistinguishable. We also found that hysteresis can naturally arise even in a simple network of neurones independently of drug equilibration.
Conclusions: Effect-site equilibration models can readily collapse hysteresis. However, this does not imply that hysteresis is solely attributable to the kinetics of drug equilibration.
Keywords: effect-site concentration; hysteresis; mechanisms of anaesthesia; modelling; pharmacokinetics.
Copyright © 2020 British Journal of Anaesthesia. Published by Elsevier Ltd. All rights reserved.
Figures


Comment in
-
Resisting neural inertia: an exercise in floccinaucinihilipilification?Br J Anaesth. 2021 Jan;126(1):31-34. doi: 10.1016/j.bja.2020.09.025. Epub 2020 Oct 26. Br J Anaesth. 2021. PMID: 33121747 No abstract available.
Similar articles
-
A stochastic basis for neural inertia in emergence from general anaesthesia.Br J Anaesth. 2018 Jul;121(1):86-94. doi: 10.1016/j.bja.2018.02.035. Epub 2018 Apr 11. Br J Anaesth. 2018. PMID: 29935600 Free PMC article.
-
Pharmacokinetic-pharmacodynamic (PK-PD) modelling in non-steady-state studies and arterio-venous drug concentration differences.Br J Clin Pharmacol. 1994 Nov;38(5):389-400. doi: 10.1111/j.1365-2125.1994.tb04372.x. Br J Clin Pharmacol. 1994. PMID: 7893578 Free PMC article.
-
Estimation of amobarbital plasma-effect site equilibration kinetics. Relevance of polyexponential conductance functions.J Pharmacokinet Biopharm. 1991 Dec;19(6):617-34. doi: 10.1007/BF01080870. J Pharmacokinet Biopharm. 1991. PMID: 1815044
-
Pharmacokinetic-pharmacodynamic modelling in anaesthesia.Br J Clin Pharmacol. 2015 Jan;79(1):72-84. doi: 10.1111/bcp.12286. Br J Clin Pharmacol. 2015. PMID: 24251846 Free PMC article. Review.
-
The role of pharmacokinetics and pharmacodynamics in clinical anaesthesia practice.Curr Opin Anaesthesiol. 2020 Aug;33(4):483-489. doi: 10.1097/ACO.0000000000000881. Curr Opin Anaesthesiol. 2020. PMID: 32530894 Review.
Cited by
-
Anesthesia and the neurobiology of consciousness.Neuron. 2024 May 15;112(10):1553-1567. doi: 10.1016/j.neuron.2024.03.002. Epub 2024 Apr 4. Neuron. 2024. PMID: 38579714 Free PMC article. Review.
-
Asymmetric neural dynamics characterize loss and recovery of consciousness.Neuroimage. 2021 Aug 1;236:118042. doi: 10.1016/j.neuroimage.2021.118042. Epub 2021 Apr 10. Neuroimage. 2021. PMID: 33848623 Free PMC article.
-
Historical and Modern Evidence for the Role of Reward Circuitry in Emergence.Anesthesiology. 2022 Jun 1;136(6):997-1014. doi: 10.1097/ALN.0000000000004148. Anesthesiology. 2022. PMID: 35362070 Free PMC article. Review.
-
The Inert Brain: Explaining Neural Inertia as Post-anaesthetic Sleep Inertia.Front Neurosci. 2021 Mar 2;15:643871. doi: 10.3389/fnins.2021.643871. eCollection 2021. Front Neurosci. 2021. PMID: 33737863 Free PMC article.
-
Time to Wake Up! The Ongoing Search for General Anesthetic Reversal Agents.Anesthesiology. 2024 Mar 1;140(3):610-627. doi: 10.1097/ALN.0000000000004846. Anesthesiology. 2024. PMID: 38349760 Free PMC article.
References
-
- Schnider T.W., Minto C.F., Shafer S.L. The influence of age on propofol pharmacodynamics. Anesthesiology. 1999;90:1502–1516. - PubMed
-
- Minto C.F., Schnider T.W., Gregg K.M., Henthorn T.K., Shafer S.L. Using the time of maximum effect site concentration to combine pharmacokinetics and pharmacodynamics. Anesthesiology. 2003;99:324–333. - PubMed
-
- Schüttler J., Stanski D.R., White P.F. Pharmacodynamic modeling of the EEG effects of ketamine and its enantiomers in man. J Pharmacokinet Biopharm. 1987;15:241–253. - PubMed
-
- Schnider T.W., Minto C.F., Gambus P.L. The influence of method of administration and covariates on the pharmacokinetics of propofol in adult volunteers. Anesthesiology. 1998;88:1170–1182. - PubMed
-
- Stanski D.R., Hudson R.J., Homer T.D., Saidman L.J., Meathe E. Pharmacodynamic modeling of thiopental anesthesia. J Pharmacokinet Biopharm. 1984;12:223–240. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

