Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Oct 13:2020:5248569.
doi: 10.1155/2020/5248569. eCollection 2020.

A Mathematical Model to Study the Effectiveness of Some of the Strategies Adopted in Curtailing the Spread of COVID-19

Isa Abdullahi Baba  1 , Bashir Abdullahi Baba  2 , Parvaneh Esmaili  2
Affiliations

A Mathematical Model to Study the Effectiveness of Some of the Strategies Adopted in Curtailing the Spread of COVID-19

Isa Abdullahi Baba et al. Comput Math Methods Med. .

Abstract

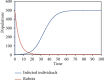
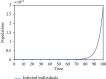
In this paper, we developed a model that suggests the use of robots in identifying COVID-19-positive patients and which studied the effectiveness of the government policy of prohibiting migration of individuals into their countries especially from those countries that were known to have COVID-19 epidemic. Two compartmental models consisting of two equations each were constructed. The models studied the use of robots for the identification of COVID-19-positive patients. The effect of migration ban strategy was also studied. Four biologically meaningful equilibrium points were found. Their local stability analysis was also carried out. Numerical simulations were carried out, and the most effective strategy to curtail the spread of the disease was shown.

PubMed Disclaimer

Conflict of interest statement

There is no conflict of interest related to this research.

Figures

Figure 1
Figure 1
The dynamics of the infected individuals when there are robots for identification of the infected individuals but there is no restriction on migration.
Figure 2
Figure 2
The dynamics of the infected individuals when there are robots for identification of the infected individuals and there is restriction on migration.
Figure 3
Figure 3
The dynamics of the infected individuals when there are no robots for identification of the infected individuals but there is restriction on migration.
Figure 4
Figure 4
The dynamics of the infected individuals when there are no robots for identification of the infected individuals and there is no restriction on migration.
See this image and copyright information in PMC

References

    1. Abramowitz M., Stegun I. A. Handbook of Mathematical Functions. New York, NY: Dover publications; 1968.
    1. Press W. H., Flannery B. P., Teukolsky S. A., Vetterling W. T. The Art of Scientific Computing. 3rd. Cambridge: Cambridge University Press; 1987. Numerical Recipes.
    1. Komarova N. L. Mathematical modeling of tumorigenesis: mission possible. Current opinion in oncology. 2005;17(1):39–43. - PubMed
    1. Gatenby R. A., Gawlinski E. T. The glycolytic phenotype in carcinogenesis and tumor invasion: insights through mathematical models. Cancer Research. 2003;63(14):3847–3854. - PubMed
    1. Breward C. J., Byrne H. M., Lewis C. E. A multiphase model describing vascular tumour growth. Bulletin of Mathematical Biology. 2003;65(4):609–640. doi: 10.1016/S0092-8240(03)00027-2. - DOI - PubMed

MeSH terms

LinkOut - more resources