What Is the Effect of Using a Competing-risks Estimator when Predicting Survivorship After Joint Arthroplasty: A Comparison of Approaches to Survivorship Estimation in a Large Registry

Abstract

Background: There is increasing interest in the development of statistical models that can be used to estimate risk of adverse patient outcomes after joint arthroplasty. Competing risk approaches have been recommended to estimate risk of longer-term revision, which is often likely to be precluded by the competing risk of death. However, a common approach is to ignore the competing risk by treating death as a censoring event and using standard survival models such as Cox regression. It is well-known that this approach can overestimate the event risk for population-level estimates, but the impact on the estimation of a patient's individualized risk after joint arthroplasty has not been explored.

Questions/purposes: We performed this study to (1) determine whether using a competing risk or noncompeting risk method affects the accuracy of predictive models for joint arthroplasty revision and (2) determine the magnitude of difference that using a competing risks versus noncompeting risks approach will make to predicted risks for individual patients.

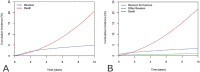
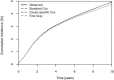
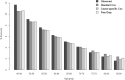
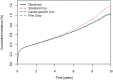
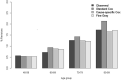
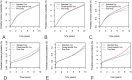
Methods: The predictive performance of a standard Cox model, with competing risks treated as censoring events, was compared with the performance of two competing risks approaches, the cause-specific Cox model and Fine-Gray model. Models were trained and tested using data pertaining to 531,304 TKAs and 274,618 THAs recorded in the Australian Orthopaedic Association National Joint Replacement Registry between January 1, 2003 and December 31, 2017. The registry is a large database with near-complete capture and follow-up of all hip and knee joint arthroplasty in Australia from 2003 onwards, making it an ideal setting for this study. The performance of the three modeling approaches was compared in two different prediction settings: prediction of the 10-year risk of all-cause revision after TKA and prediction of revision for periprosthetic fracture after THA. The calibration and discrimination of each approach were compared using the concordance index, integrated Brier scores, and calibration plots. Calibration of 10-year risk estimates was further assessed within subgroups of age by comparing the observed and predicted proportion of events. Estimated 10-year risks from each model were also compared in three hypothetical patients with different risk profiles to determine whether differences in population-level performance metrics would translate into a meaningful difference for individual patient predictions.

Results: The standard Cox and two competing risks models showed near-identical ability to distinguish between high-risk and low-risk patients (c-index 0.64 [95% CI, 0.64 to 0.64] for all three modeling approaches for TKAs and 0.66 [95% CI 0.66 to 0.66] for THA). All models performed similarly in patients younger than 75 years, but for patients aged 75 years and older, the standard Cox model overestimated the risk of revision more than the cause-specific Cox and Fine-Gray model did. These results were echoed when predictions were made for hypothetical individual patients. For patients with a low competing risk of mortality, the 10-year predicted risks from the standard Cox, cause-specific Cox, and Fine-Gray models were similar for TKAs and THAs. However, a larger difference was observed for hypothetical 89-year-old patients with increased mortality risk. In TKAs, the revision risk for an 89-year-old patient was so low that this difference was negligible (0.83% from the cause-specific Cox model versus 1.1% from the standard Cox model). However, for THAs, where older age is a risk factor for both death and revision for periprosthetic fracture, a larger difference was observed in the 10-year predicted risks for a hypothetical 89-year-old patient (3.4% from the cause-specific Cox model versus 5.2% from the standard Cox model).

Conclusion: When developing models to predict longer-term revision of joint arthroplasty, failing to use a competing risks modeling approach will result in overestimating the revision risk for patients with a high risk of mortality during the surveillance period. However, even in an extreme instance, where both the frequency of the event of interest and the competing risk of death are high, the largest absolute difference in predicted 10-year risk for an individual patient was just 1.8%, which may not be of consequence to an individual. Despite these findings, when developing or using risk prediction models, researchers and clinicians should be aware of how competing risks were handled in the modeling process, particularly if the model is intended for use populations where the mortality risk is high.

Level of evidence: Level III, therapeutic study.

Fig. 1.

A-B Flowchart showing exclusion criteria for (A) TKA and (B) THA procedures included in the analysis.

Fig. 2.

A-B Cumulative incidence of (A) revision and death following TKA, and (B) revision for periprosthetic fracture, other causes of revision, and death after THA. A color image accompanies the online version of this article.

Fig. 3

Overall calibration is assessed for TKA by comparing the observed proportion of revisions to the predicted event probabilities calculated using the standard Cox, cause-specific Cox, and Fine-Gray modeling approaches. A color image accompanies the online version of this article.

Fig. 4

Age-specific calibration is assessed by comparing the observed and predicted proportion of events for the standard Cox, cause-specific Cox, and Fine-Gray model for revision risk after TKA

Fig. 5

Overall calibration is assessed for THA by comparing the observed proportion of revisions for fracture to the predicted event probabilities calculated using the standard Cox, cause-specific Cox, and Fine-Gray modeling approaches. A color image accompanies the online version of this article.

Fig. 6

Age-specific calibration is assessed by comparing the observed and predicted proportion of events for the standard Cox, cause-specific Cox, and Fine-Gray model for risk of revision for periprosthetic fracture after THA

Fig. 7.

A-F The predicted risk for hypothetical individual patients from the standard Cox, cause-specific Cox, and Fine-Gray models are compared over time for (A) a patient at a high risk of having TKA revision, (B) a patient with an average risk of having TKA revision, (C) a patient with a low risk of having TKA revision, (D) a patient with a low risk of having a fracture after THA, (E) a patient with an average risk of having a fracture after THA, and (F) a patient with a high risk of having a fracture after THA. A color image accompanies the online version of this article.