Analysis of streaming potential flow and electroviscous effect in a shear-driven charged slit microchannel

Abstract

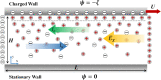
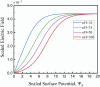
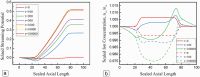
Investigating the flow behavior in microfluidic systems has become of interest due to the need for precise control of the mass and momentum transport in microfluidic devices. In multilayered-flows, precise control of the flow behavior requires a more thorough understanding as it depends on multiple parameters. The following paper proposes a microfluidic system consisting of an aqueous solution between a moving plate and a stationary wall, where the moving plate mimics a charged oil-water interface. Analytical expressions are derived by solving the nonlinear Poisson-Boltzmann equation along with the simplified Navier-Stokes equation to describe the electrokinetic effects on the shear-driven flow of the aqueous electrolyte solution. The Debye-Huckel approximation is not employed in the derivation extending its compatibility to high interfacial zeta potential. Additionally, a numerical model is developed to predict the streaming potential flow created due to the shear-driven motion of the charged upper wall along with its associated electric double layer effect. The model utilizes the extended Nernst-Planck equations instead of the linearized Poisson-Boltzmann equation to accurately predict the axial variation in ion concentration along the microchannel. Results show that the interfacial zeta potential of the moving interface greatly impacts the velocity profile of the flow and can reverse its overall direction. The numerical results are validated by the analytical expressions, where both models predicted that flow could reverse its overall direction when the interfacial zeta potential of the oil-water is above a certain threshold value. Finally, this paper describes the electroviscous effect as well as the transient development of electrokinetic effects within the microchannel.

Figure 1

Schematic of the 2D geometry of the charged slit microchannel used for analytical modeling.

Figure 2

Meshing and boundary conditions for (a) momentum equation, (b) Poisson’s equation, and (c) Nernst–Planck equations.

Figure 3

(a) Distribution electric potential, and (b) distribution of co-ions and counter ions within the channel where the dashed lines are for the co-ions while the solid lines are for the counterions (κH = 10).

Figure 4

Variation of the F_CS with surface potential for different κH.

Figure 5

Variation of the induced electric field (E_x) vs. non-dimensional surface potential (Ψ_S) at different κH.

Figure 6

Effect of surface potential (${\mathrm{\Psi }}_s$) on non-dimensional velocity profile, (a) κH = 10, (b) κH = 100.

Figure 7

(a) A plot of non-dimensional flow rate versus κH for different surface potentials; (b) plot of normalized viscosity $\frac{{\mathit{\mu }}_{\mathit{a}}}{\mathit{\mu }}$ versus κH The flow rate was scaled by the volumetric flow rate in the simple shear driven flow case with the absence of any electrokinetic effect Q_scaling = UH/2.

Figure 8

(a) Comparison of the numerical and analytical predictions of the induced electric field for different surface potentials, κH = 10. (b) Scaled electric field distribution, κH = 10. For a comparison of the numerical and analytical predictions of the induced electric field for κH = 100 (see Supplementary Figure S1).

Figure 9

Comparison of the numerical (circles) and analytical predictions (squares) of the scaled flow rates for different surface potentials, κH = 10. The normalized numerical flow rates (triangles) is the normalized flow rate by the numerical result at Ψ_s = 0 (finite microchannel with simple shear driven flow case).

Figure 10

Velocity profile across the non-dimensional channel height for (a) Ψ_s = 1, and (b) Ψ_s = 6. The velocity field was obtained for κH = 10.

Figure 11

(a) Development of streaming potential along the centerline of the channel, (b) scaled ion concentration along the centerline of the channel, the dashed line represents the co-ion concentration while the solid lines are for the counterion concentration. κH = 10 and Ψ_S = 1.

Figure 12

Contour plot of scaled co-ions concentration within the microchannel with a zoomed-in inset of the region near the charged wall highlighting the asymmetric axial variation of the electric double layer. κH = 10 and Ψ_S = 1.