Marriage and Health: Selection, Protection, and Assortative Mating
- PMID: 33132405
- PMCID: PMC7597938
- DOI: 10.1016/j.euroecorev.2018.02.005
Marriage and Health: Selection, Protection, and Assortative Mating
Abstract
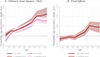
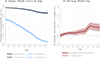
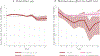
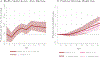
Using data from the Panel Study of Income Dynamics (PSID) and the Medical Expenditure Panel Survey (MEPS), we analyze the health gap between married and unmarried individuals of working-age. Controlling for observables, we find a gap that peaks at 10 percentage points at ages 55-59 years. The marriage health gap is similar for men and women. If we allow for unobserved heterogeneity in innate health (permanent and age-dependent), potentially correlated with timing and likelihood of marriage, we find that the effect of marriage on health disappears below age 40 years, while about 5 percentage points difference between married and unmarried individuals remains at older ages (55-59 years). This indicates that the observed gap is mainly driven by selection into marriage at younger ages, but there might be a protective effect of marriage at older ages. Exploring the mechanisms behind this result, we find that better innate health is associated with a higher probability of marriage and a lower probability of divorce, and there is strong assortative mating among couples by innate health. We also find that married individuals are more likely to have a healthier behavior compared to unmarried ones. Finally, we find that health insurance is critical for the beneficial effect of marriage.
Keywords: Assortative Mating; Grouped-Fixed-Effects Estimator; Health; I10; I12; Innate Health; J10; Marriage; Panel Data; Protective Effect of Marriage.
Figures







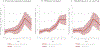


References
-
- Adams Peter, Hurd Michael D., McFadden Daniel, Merrill Angela, and Ribeiro Tiago, “Healthy, wealthy, and wise? Tests for direct causal paths between health and socioeconomic status,” Journal of Econometrics, January 2003, 112 (1), 356.
-
- Agency of Healthcare Research and Quality, “Medical Expenditure Panel Survey,” household component, public use data set. Produced and Distributed by The Agency for Healthcare Research and Quality 2011.
-
- Aizer Ayal A., Chen Ming-Hui, McCarthy Ellen P., Mendu Mallika L., Koo Sophia, Wilhite Tyler J., Graham Powell L., Choueiri Toni K., Hoffman Karen E., Martin Neil E., Hu Jim C., and Nguyen Paul L., “Marital Status and Survival in Patients With Cancer,” Journal of Clinical Oncology, November 2013, 31 (31), 3869–3876. - PMC - PubMed
-
- Anderson Michael, Dobkin Carlos, and Gross Tal, “The Effect of Health Insurance Coverage on the Use of Medical Services,” American Economic Journal: Economic Policy, February 2012, 4 (1), 1–27.
-
- Arellano Manuel and Bover Olympia, “Another Look at the Instrumental Variable Estimation of Error-Components Models,” Journal of Econometrics, July 1995, 68 (1), 29–51.
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
