Selecting a Scale for Spatial Confounding Adjustment
- PMID: 33132544
- PMCID: PMC7592711
- DOI: 10.1111/rssa.12556
Selecting a Scale for Spatial Confounding Adjustment
Abstract
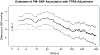
Unmeasured, spatially-structured factors can confound associations between spatial environmental exposures and health outcomes. Adding flexible splines to a regression model is a simple approach for spatial confounding adjustment, but the spline degrees of freedom do not provide an easily interpretable spatial scale. We describe a method for quantifying the extent of spatial confounding adjustment in terms of the Euclidean distance at which variation is removed. We develop this approach for confounding adjustment with splines and using Fourier and wavelet filtering. We demonstrate differences in the spatial scales these bases can represent and provide a comparison of methods for selecting the amount of confounding adjustment. We find the best performance for selecting the amount of adjustment using an information criterion evaluated on an outcome model without exposure. We apply this method to spatial adjustment in an analysis of fine particulate matter and blood pressure in a cohort of United States women.
Keywords: Air Pollution Epidemiology; Confounding; Regression Splines; Spatial Filtering.
Figures
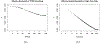



References
-
- Akaike H (1973). Information theory and an extension of the maximum likelihood principle In Petrov B and Csaki F (Eds.), Second International Symposium on Information Theory, pp. 267–281. Budapest: Akademiai Kiado.
-
- Besag J, York J, and Mollié A (1991). Bayesian image restoration with two applications in spatial statistics. Annals of the Institute of Statistical Mathematics 43(1), 1–20.
-
- Burger W and Burge JM (2009). Principles of Digital Image Processing: Core Algorithms. London: Springer.
Grants and funding
LinkOut - more resources
Full Text Sources
