Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020:50:361-372.
doi: 10.1016/j.arcontrol.2020.10.005. Epub 2020 Oct 26.

A time-varying SIRD model for the COVID-19 contagion in Italy

Giuseppe C Calafiore  1   2 , Carlo Novara  1 , Corrado Possieri  3
Affiliations

A time-varying SIRD model for the COVID-19 contagion in Italy

Giuseppe C Calafiore et al. Annu Rev Control. 2020.

Abstract

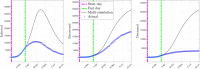
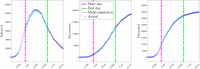
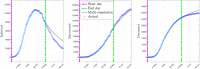
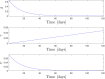
The purpose of this work is to give a contribution to the understanding of the COVID-19 contagion in Italy. To this end, we developed a modified Susceptible-Infected-Recovered-Deceased (SIRD) model for the contagion, and we used official data of the pandemic for identifying the parameters of this model. Our approach features two main non-standard aspects. The first one is that model parameters can be time-varying, allowing us to capture possible changes of the epidemic behavior, due for example to containment measures enforced by authorities or modifications of the epidemic characteristics and to the effect of advanced antiviral treatments. The time-varying parameters are written as linear combinations of basis functions and are then inferred from data using sparse identification techniques. The second non-standard aspect resides in the fact that we consider as model parameters also the initial number of susceptible individuals, as well as the proportionality factor relating the detected number of positives with the actual (and unknown) number of infected individuals. Identifying the model parameters amounts to a non-convex identification problem that we solve by means of a nested approach, consisting in a one-dimensional grid search in the outer loop, with a Lasso optimization problem in the inner step.

Keywords: Contagion modeling; Covid-19; Lasso; SIR models.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Fig. 1
Fig. 1
Overall evolution of the COVID-19 contagion in Italy. Daily deaths and scaled number of active infected individuals (national data for Italy). The I(t) scaling factor is 0.014.
Fig. 2
Fig. 2
Objective cost as a function of q in the early stage model.
Fig. 3
Fig. 3
Multi-simulation prediction with the early stage model (constant parameters).
Fig. 4
Fig. 4
Multi-simulation prediction with the late stage model (constant parameters).
Fig. 5
Fig. 5
Multi-simulation prediction with the full data model (constant parameters).
Fig. 6
Fig. 6
Identified shape of the parameters for national data. Time is expressed in days since Feb. 24, 2020.
Fig. 7
Fig. 7
Multi-simulation prediction with the time-varying model (national data).
Fig. 8
Fig. 8
Identified shape of the parameters for regional data. Time is expressed in days since Feb. 24, 2020.
Fig. 9
Fig. 9
Multi-simulation prediction with the time-varying model for regional data.
Fig. 10
Fig. 10
Ratio between Intensive Care and Infected individuals (national data).
See this image and copyright information in PMC

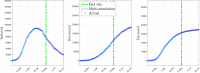
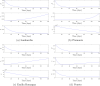
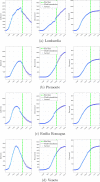
References

    1. Bailey N.T.J. 2nd ed. Hafner Press; New York, NY, USA: 1975. The mathematical theory of infectious diseases and its applications.
    1. Brauer F. Mathematical epidemiology: Past, present, and future. Infectious Disease Modelling. 2017;2(2):113–127. - PMC - PubMed
    1. Caccavo, D. (2020). Chinese and italian COVID-19 outbreaks can be correctly described by a modified SIRD model. medRxiv.
    1. Casella, F. (2020). Can the COVID-19 epidemic be managed on the basis of daily data?arXiv preprint arXiv:2003.06967.
    1. Chowell G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts. Infectious Disease Modelling. 2017;2(3):379–398. doi: 10.1016/j.idm.2017.08.001. - DOI - PMC - PubMed

LinkOut - more resources