The effect of heterogeneity on hypergraph contagion models

Abstract

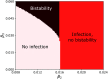
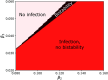
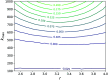
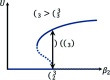
The dynamics of network social contagion processes such as opinion formation and epidemic spreading are often mediated by interactions between multiple nodes. Previous results have shown that these higher-order interactions can profoundly modify the dynamics of contagion processes, resulting in bistability, hysteresis, and explosive transitions. In this paper, we present and analyze a hyperdegree-based mean-field description of the dynamics of the susceptible-infected-susceptible model on hypergraphs, i.e., networks with higher-order interactions, and illustrate its applicability with the example of a hypergraph where contagion is mediated by both links (pairwise interactions) and triangles (three-way interactions). We consider various models for the organization of link and triangle structures and different mechanisms of higher-order contagion and healing. We find that explosive transitions can be suppressed by heterogeneity in the link degree distribution when links and triangles are chosen independently or when link and triangle connections are positively correlated when compared to the uncorrelated case. We verify these results with microscopic simulations of the contagion process and with analytic predictions derived from the mean-field model. Our results show that the structure of higher-order interactions can have important effects on contagion processes on hypergraphs.

FIG. 1.

Illustration of a hypergraph. Infected nodes (red) infect a healthy node (gray) via hyperedges of sizes 2 and 3 with rates ${\beta }_2$ and ${\beta }_3$, respectively.

FIG. 2.

Schematic illustration of the degree-correlated and uncorrelated cases. In the degree-correlated case (left), nodes with more links are more likely to belong to a triangle. In the uncorrelated case (right), triangles connect nodes with a probability independent of their degree.

FIG. 3.

Fraction of infected nodes $U$ vs link infectivity ${\beta }_2$ obtained from the mean-field equations (15) and (16) (solid and dashed lines) and from microscopic simulations (connected circles) using $P(k)\propto k^{-4}$ on $[67,1000]$, $\gamma =2$, and $N=10000$ for ${\beta }_3=0.0194$ (a), $0.0388$ (b), and $0.05482$ (c). Refer to the text for an explanation of the discrepancy between the mean-field equations and microscopic simulations.

FIG. 4.

Phase diagram for the degree-correlated, collective contagion model. The light pink region labeled “No infection” corresponds to $1$ solution of Eq. (10), the orange region labeled “Infection, no bistability” to $2$ solutions, and the region labeled “Bistability” to $3$ solutions. The parameters are $\gamma =2$ and $P(k)\propto k^{-4}$ when $67<k<1000$ and $0$ otherwise.

FIG. 5.

Bistability index $B$ as a function of ${\beta }_3$ for (a) $P(k)$ constant for $50<k<150$ and 0 otherwise, (b) $P(k)\propto k^{-4}$ for $67<k<1000$ and 0 otherwise, and (c) $P(k)\propto k^{-3}$ for $53<k<1000$ and 0 otherwise. For each distribution, we considered the uncorrelated case (orange connected circles) and the degree correlated case (blue connected triangles). The dashed lines indicate the value ${\beta }_3^c$ at which we expect the onset of bistability, obtained from numerical solution of the mean-field equations (12) and (15)–(16).

FIG. 6.

Phase diagram for the degree-correlated, individual contagion model with parameters $\gamma =2$ and $P(k)\propto k^{-4}$ when $67<k<1000$ and $0$ otherwise.

FIG. 7.

Phase diagram for the degree-correlated, higher-order healing with individual contagion with parameters $\gamma =2$ and $P(k)\propto k^{-4}$ when $67<k<1000$ and $0$ otherwise.

FIG. 8.

${\beta }_3^c/{\beta }_2^c$ as a function of power-law distribution parameters for the degree-correlated case (a) and the uncorrelated case (b). ${\beta }_3^c$ was calculated numerically from the mean-field equations (see the Appendix) and ${\beta }_2^c=\gamma ⟨k⟩/⟨k^2⟩$. The parameters are $P(k)\propto k^{-r}$ if $50\le k\le k_{max}$ and $P(k)=0$ otherwise and $\gamma =2$.

FIG. 9.

Relative error in the value of ${\beta }_3^c/{\beta }_2^c$ obtained from Eq. (43) compared with the numerically obtained value shown in Fig. 8(b).

FIG. 10.

Illustration of the bistability index with respect to the solutions to the mean-field equation in the bistable regime.