Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Oct;148(4):2161.
doi: 10.1121/10.0002163.

Study of spatiotemporal liquid dynamics in a vibrating vocal fold by using a self-oscillating poroelastic model

Austin Scholp  1 , Caroline Jeddeloh  1 , Chao Tao  2 , Xiaojun Liu  3 , Seth H Dailey  1 , Jack J Jiang  1
Affiliations

Study of spatiotemporal liquid dynamics in a vibrating vocal fold by using a self-oscillating poroelastic model

Austin Scholp et al. J Acoust Soc Am. 2020 Oct.

Abstract

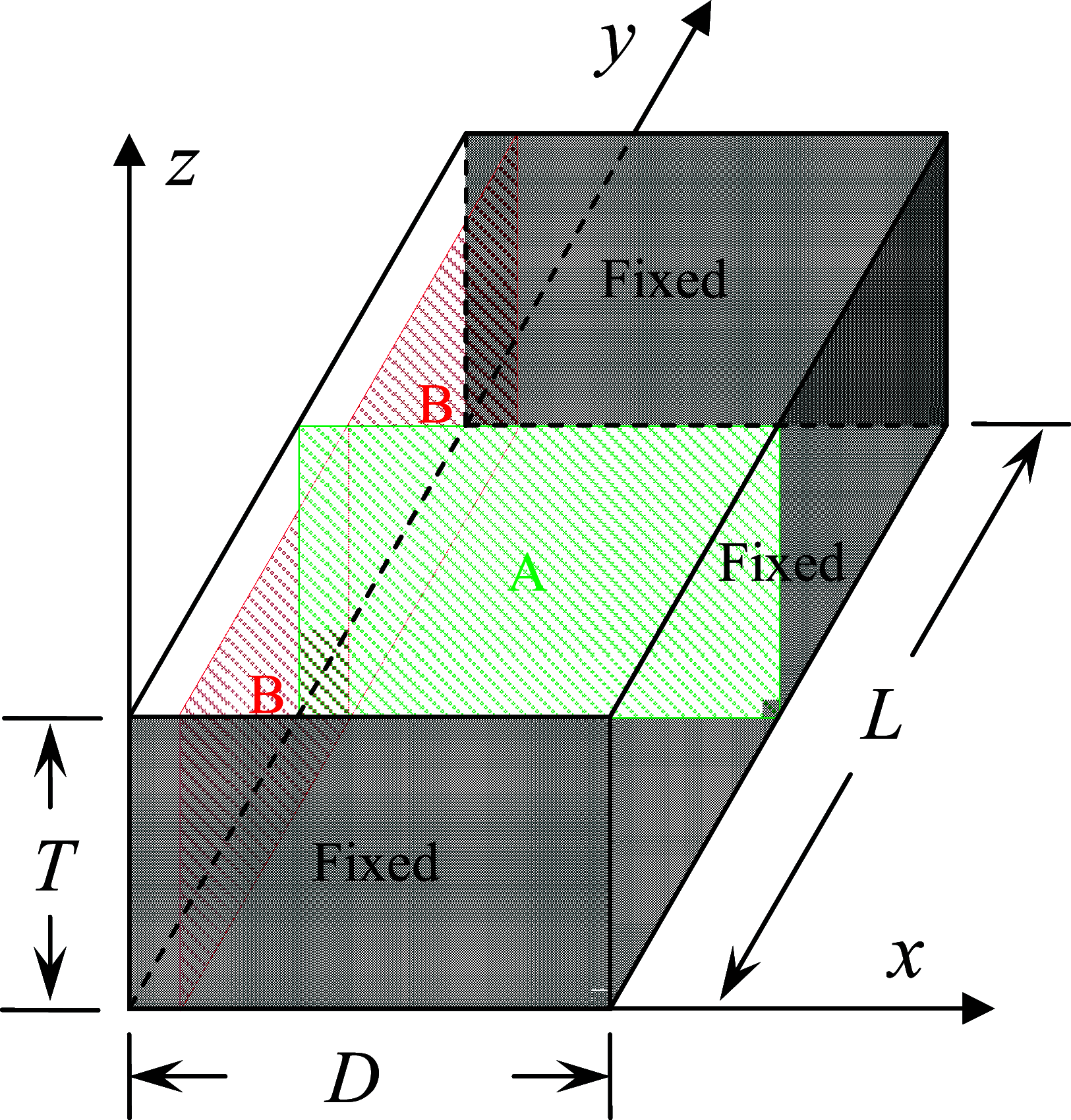
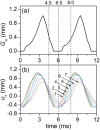
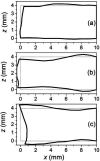
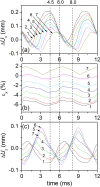
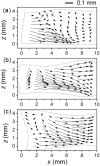
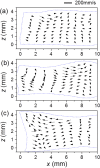
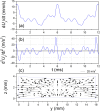
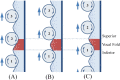
The main purpose of this study is to investigate the spatiotemporal interstitial fluid dynamics in a vibrating vocal fold. A self-oscillating poroelastic model is proposed to study the liquid dynamics in the vibrating vocal folds by treating the vocal fold tissue as a transversally isotropic, fluid-saturated, porous material. Rich spatiotemporal liquid dynamics have been found. Specifically, in the vertical direction, the liquid is transported from the inferior side to the superior side due to the propagation of the mucosal wave. In the longitudinal direction, the liquid accumulates at the anterior-posterior midpoint. However, the contact between the two vocal folds forces the accumulated liquid out laterally in a very short time span. These findings could be helpful for exploring etiology of some laryngeal pathologies, optimizing laryngeal disease treatment, and understanding hemodynamics in the vocal folds.

PubMed Disclaimer

Figures

FIG. 1.
FIG. 1.
(Color online) A diagram of the vocal fold model, where T, D, and L represent the thickness, depth, and length of the vocal fold, respectively. The fixed boundary condition was applied on the gray surfaces (the anterior surface, the posterior surface, and the lateral surface). The free boundary condition was applied on the top surface (x–y plane at z = T) and the bottom surface (x–y plane at z = 0). A drive force based on Bernoulli's law was applied on the medial surface (the y–z plane at x = 0) to generate the self-vibration of this model. The plane A, filled with a slash pattern, is located at the AP midpoint, where y = 0.8 cm. The plane B, also filled with a slash pattern, is located at x = 0.1 cm, which is just below the medial surface and represents one plane in the vocal cover.
FIG. 2.
FIG. 2.
(Color online) Glottal width and the mucosal wave propagation with a subglottal pressure Ps = 0.8 kPa (≈ 8 cm H2O). Here, we have removed an initial transient behavior with a length of 2 s to ensure purely cyclic behavior. (a) The wave form of the glottal width (Gw) between the two vocal folds. (b) The lateral displacement (ux) of wave forms at the AP midpoint of the medial surface, where curves 1, 2, 3, 4, 5, 6, 7 correspond to nodes at z = 1.2, 1.6, 2.0, 2.4, 2.8, 3.2, and 3.6 mm, respectively. In this figure, the three dotted lines correspond to t = 4.5 ms (before collision), t = 6.0 ms (in the process of collision), t = 8.0 ms (after collision).
FIG. 3.
FIG. 3.
The profiles of the cross section A at three moments during vocal fold vibration, where figures (a), (b), and (c) correspond to the moments before collision (t = 4.5 ms), in the process of collision (t = 6.0 ms), and after collision (t = 8.0 ms), respectively.
FIG. 4.
FIG. 4.
(Color online) The waveform of the liquid component in a vibrating vocal fold. The curves 1–7 correspond to seven nodes at the AP midpoint of the subsurface B. Their coordinates are (x, y, z) = (0.1, 0.8, zi) cm, where zi = 1.2, 1.6, 2.0, 2.4, 2.8, 3.2, and 3.6 with i = 1–7. (a) The relative displacement in the lateral direction, where ΔUx = Ux – ux. (b) The longitudinal liquid strain (εy = dUy/dy), where a positive liquid strain indicates that the liquid is squeezed out, and a negative εy means there is liquid accumulation. (c) The relative displacement in the vertical direction, where ΔUz = Uz – uz.
FIG. 5.
FIG. 5.
(Color online) Relative fluid displacement on the cross-section A, where the arrows in the vocal fold profile represent the relative displacement vector ΔU = U – u. (a) The moment before collision (t = 4.5 ms). (b) The moment in the process of collision (t = 6.0 ms). (c) The moment after collision (t = 8.0 ms).
FIG. 6.
FIG. 6.
(Color online) Relative fluid velocity in the cross-section A, where the arrows represent the relative velocity vector ΔV = V – v. (a) The moment before collision (t = 4.5 ms). (b) The moment in the process of collision (t = 6.0 ms). (c) The moment after collision (t = 8.0 ms).
FIG. 7.
FIG. 7.
(Color online) Relative liquid displacement in the cross-section B. (a) The moment before collision (t = 4.5 ms). (b) The moment in the process of collision (t = 6.0 ms). (c) The moment after collision (t = 8.0 ms).
FIG. 8.
FIG. 8.
(Color online) Relative liquid velocity in the cross-section B. (a) The moment before collision (t = 4.5 ms). (b) The moment in the process of collision (t = 6.0 ms). (c) The moment after collision (t = 8.0 ms).
FIG. 9.
FIG. 9.
(Color online) Relative liquid acceleration in vibrating vocal folds. (a) The longitudinal liquid velocity, near the midpoint. Positive velocity represents the direction moving away from the midpoint. (b) The longitudinal liquid acceleration. Positive acceleration represents the direction moving away from the midpoint. (c) The relative liquid acceleration at the moment of collision (t = 6.0 ms).
FIG. 10.
FIG. 10.
(Color online) Schematic drawing of the liquid transport induced by the mucosal wave propagation. (a) Stage 1, (b) stage 2, (c) stage 3.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Titze I. R., “ On the mechanics of vocal-fold vibration,” J. Acoust. Soc. Am. 60, 1366–1380 (1976).10.1121/1.381230 - DOI - PubMed
    1. Jiang J. J., C. E., Diaz , and Hanson D. G., “ Finite element modeling of vocal fold vibration in normal phonation and hyper functional dysphonia: Implications for the pathogenesis of vocal nodules,” Ann. Otol. Rhinol. Laryngol. Suppl. 107, 603–610 (1998).10.1177/000348949810700711 - DOI - PubMed
    1. Alipour F., Berry D. A., and Titze I. R., “ A finite-element model of vocal-fold vibration,” J. Acoust. Soc. Am. 108, 3003–3012 (2000).10.1121/1.1324678 - DOI - PubMed
    1. Hunter E. J., Titze I. R., and Alipour F., “ A three-dimensional model of vocal fold abduction/adduction,” J. Acoust. Soc. Am. 115, 1747–1759 (2004).10.1121/1.1652033 - DOI - PMC - PubMed
    1. Gunter H. E., “ A mechanical model of vocal-fold collision with high spatial and temporal resolution,” J. Acoust. Soc. Am. 113, 994–1000 (2003).10.1121/1.1534100 - DOI - PubMed

Publication types