G-computation for policy-relevant effects of interventions on time-to-event outcomes

Abstract

Background: Parametric g-computation is an analytic technique that can be used to estimate the effects of exposures, treatments and interventions; it relies on a different set of assumptions than more commonly used inverse probability weighted estimators. Whereas prior work has demonstrated implementations for binary exposures and continuous outcomes, use of parametric g-computation has been limited due to difficulty in implementation in more typical complex scenarios.

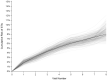
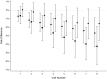
Methods: We provide an easy-to-implement algorithm for parametric g-computation in the setting of a dynamic baseline intervention of a baseline exposure and a time-to-event outcome. To demonstrate the use of our algorithm, we apply it to estimate the effects of interventions to reduce area deprivation on the cumulative incidence of sexually transmitted infections (STIs: gonorrhea, chlamydia or trichomoniasis) among women living with HIV in the Women's Interagency HIV Study.

Results: We found that reducing area deprivation by a maximum of 1 tertile for all women would lead to a 2.7% [95% confidence interval (CI): 0.1%, 4.3%] reduction in 4-year STI incidence, and reducing deprivation by a maximum of 2 tertiles would lead to a 4.3% (95% CI: 1.9%, 6.4%) reduction.

Conclusions: As analytic methods such as parametric g-computation become more accessible, epidemiologists will be able to estimate policy-relevant effects of interventions to better inform clinical and public health practice and policy.

Keywords: Causal inference; G-computation; HIV; area deprivation; sexually transmitted infections; survival analysis.

Figure 1.

Algorithm for estimating the effects of a dynamic baseline intervention on a time-to-event outcome using g-computation.

Figure 2.

Comparison of the observed and modelled cumulative incidence of STIs among women with HIV in the Women's Interagency HIV Study, 2013–2018. Black line, cumulative incidence function estimated using parametric models; grey lines, cumulative incidence functions estimated nonparametrically from 200 bootstrap replicates from the original data.

Figure 3.

Cumulative incidence of STIs under interventions to reduce area-level deprivation among women with HIV in the Women’s Interagency HIV Study, 2013–2018. Thin line, no intervention; medium line, reduce area-level deprivation by 1 tertile; thick line, reduce area-level deprivation by 2 tertiles. Lines are point estimates, shaded regions are 95% CIs.

Figure 4.

Risk differences comparing the risk of STIs under interventions to reduce area-level deprivation among women with HIV in the Women’s Interagency HIV Study, 2013–2018. Circle, reduce area-level deprivation by 1 tertile vs no intervention; square, reduce area-level deprivation by 2 tertiles vs no intervention; star, reduce area-level deprivation by 1 tertile vs reduce area-level deprivation by 2 tertiles. Symbols are point estimates, bars are 95% CIs.