Analysis of a 180-degree U-turn maneuver executed by a hipposiderid bat

Abstract

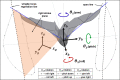
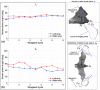
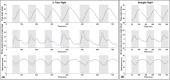
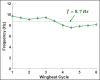
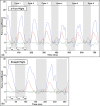
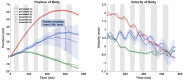
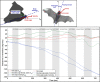
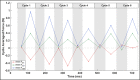
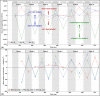
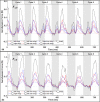
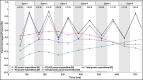
Bats possess wings comprised of a flexible membrane and a jointed skeletal structure allowing them to execute complex flight maneuvers such as rapid tight turns. The extent of a bat's tight turning capability can be explored by analyzing a 180-degree U-turn. Prior studies have investigated more subtle flight maneuvers, but the kinematic and aerodynamic mechanisms of a U-turn have not been characterized. In this work, we use 3D optical motion capture and aerodynamic simulations to investigate a U-turn maneuver executed by a great roundleaf bat (Hipposideros armiger: mass = 55 g, span = 51 cm). The bat was observed to decrease its flight velocity and gain approximately 20 cm of altitude entering the U-turn. By lowering its velocity from 2.0 m/s to 0.5 m/s, the centripetal force requirement to execute a tight turn was substantially reduced. Centripetal force was generated by tilting the lift force vector laterally through banking. During the initiation of the U-turn, the bank angle increased from 20 degrees to 40 degrees. During the initiation and persisting throughout the U-turn, the flap amplitude of the right wing (inside of the turn) increased relative to the left wing. In addition, the right wing moved more laterally closer to the centerline of the body during the end of the downstroke and the beginning of the upstroke compared to the left wing. Reorientation of the body into the turn happened prior to a change in the flight path of the bat. Once the bat entered the U-turn and the bank angle increased, the change in flight path of the bat began to change rapidly as the bat negotiated the apex of the turn. During this phase of the turn, the minimum radius of curvature of the bat was 5.5 cm. During the egress of the turn, the bat accelerated and expended stored potential energy by descending. The cycle averaged total power expenditure by the bat during the six wingbeat cycle U-turn maneuver was 0.51 W which was approximately 40% above the power expenditure calculated for a nominally straight flight by the same bat. Future work on the topic of bat maneuverability may investigate a broader array of maneuvering flights characterizing the commonalities and differences across flights. In addition, the interplay between aerodynamic moments and inertial moments are of interest in order to more robustly characterize maneuvering mechanisms.

Fig 1. Ground and body coordinate systems.

Rotations relative to the body frame are defined as roll, pitch, and yaw as depicted. A stroke plane is defined for the right and left wings separately by connecting the shoulder point with a regression line passing through the locus of wingtip points.

Fig 2

Top: Body trajectory of the bat during the U-turn flight from the top and side view. Bottom: Velocity, angle of ascent, and curvature of the turn. The curvature is defined using the standard definition: (radius of curvature)^-1. The grey shaded regions denote upstrokes, and one complete wingbeat cycle consists of the upstroke+downstroke.

Fig 3

The vertical (a) and horizontal (b) stroke plane angle are shown for the right and left wing separately at each half-cycle as defined in the schematic above.

Fig 4

The motion of the wings relative to the stroke plane are characterized by the flap angle, stroke plane deviation angle, and the half-span for the 180 degree U-turn flight (a) and a straight flight (b) for comparison.

Fig 5. Wingbeat frequency by half-stroke.

The mean frequency over the flight is 8.7 Hz.

Fig 6

Trajectory of the wingtip and wrist for each wingbeat cycle of the U-turn shown in the body fixed coordinate system (a). A comparison from a representative straight flight is also provided (b).

Fig 7

Force coefficients in the body frame for the U-turn flight (a). For comparison, results from a straight flight by the same bat is also provided (b).

Fig 8. Comparison of observed and predicted position and velocity of the bat body.

Fig 9. Rotational orientation of the bat using both body-based angles (roll, elevation, and yaw) and velocity-based angles (bearing angle and climb angle).

Fig 10. Tangential, radial, and vertical components of aerodynamic force relative to the flight trajectory.

Fig 11

Half-cycle mean aerodynamic moments relative to the approximate center of mass calculated from the aerodynamic forces (a). Half-cycle mean angular acceleration of the bat body defined as rate of change of rotational velocity about the body-fixed coordinate axes (b).

Fig 12

Thrust force (a) and lift force (b) calculated in the body-fixed frame partitioned by where the force is acting. Solid lines represent right and left wing totals. The dashed and dashed-dotted lines represent the force acting on the outer and inner right and left wings.

Fig 13. Total power expenditure defined as the sum of aerodynamic power, kinetic energy expenditure, and potential energy expenditure.