PPM-Decay: A computational model of auditory prediction with memory decay
- PMID: 33147209
- PMCID: PMC7668605
- DOI: 10.1371/journal.pcbi.1008304
PPM-Decay: A computational model of auditory prediction with memory decay
Erratum in
-
Correction: PPM-Decay: A computational model of auditory prediction with memory decay.PLoS Comput Biol. 2021 May 26;17(5):e1008995. doi: 10.1371/journal.pcbi.1008995. eCollection 2021 May. PLoS Comput Biol. 2021. PMID: 34038404 Free PMC article.
Abstract
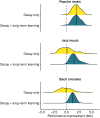
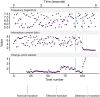
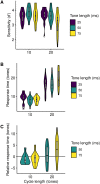
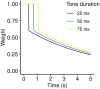
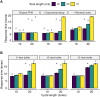
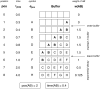
Statistical learning and probabilistic prediction are fundamental processes in auditory cognition. A prominent computational model of these processes is Prediction by Partial Matching (PPM), a variable-order Markov model that learns by internalizing n-grams from training sequences. However, PPM has limitations as a cognitive model: in particular, it has a perfect memory that weights all historic observations equally, which is inconsistent with memory capacity constraints and recency effects observed in human cognition. We address these limitations with PPM-Decay, a new variant of PPM that introduces a customizable memory decay kernel. In three studies-one with artificially generated sequences, one with chord sequences from Western music, and one with new behavioral data from an auditory pattern detection experiment-we show how this decay kernel improves the model's predictive performance for sequences whose underlying statistics change over time, and enables the model to capture effects of memory constraints on auditory pattern detection. The resulting model is available in our new open-source R package, ppm (https://github.com/pmcharrison/ppm).
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures





Similar articles
-
Information-Theoretic Properties of Auditory Sequences Dynamically Influence Expectation and Memory.Cogn Sci. 2018 Jan;42(1):43-76. doi: 10.1111/cogs.12477. Epub 2017 Jan 25. Cogn Sci. 2018. PMID: 28121017
-
Recency and suffix effects in serial recall of musical stimuli.J Exp Psychol Learn Mem Cogn. 1986 Oct;12(4):517-24. doi: 10.1037//0278-7393.12.4.517. J Exp Psychol Learn Mem Cogn. 1986. PMID: 2945898
-
Implicit learning of tonality: a self-organizing approach.Psychol Rev. 2000 Oct;107(4):885-913. doi: 10.1037/0033-295x.107.4.885. Psychol Rev. 2000. PMID: 11089410
-
Predictive information processing in music cognition. A critical review.Int J Psychophysiol. 2012 Feb;83(2):164-75. doi: 10.1016/j.ijpsycho.2011.12.010. Epub 2012 Jan 12. Int J Psychophysiol. 2012. PMID: 22245599 Review.
-
A Review of Auditory Prediction and Its Potential Role in Tinnitus Perception.J Am Acad Audiol. 2018 Jun;29(6):533-547. doi: 10.3766/jaaa.17025. J Am Acad Audiol. 2018. PMID: 29863467 Review.
Cited by
-
Implicit auditory memory in older listeners: From encoding to 6-month retention.Curr Res Neurobiol. 2023 Nov 7;5:100115. doi: 10.1016/j.crneur.2023.100115. eCollection 2023. Curr Res Neurobiol. 2023. PMID: 38020808 Free PMC article.
-
Correction: PPM-Decay: A computational model of auditory prediction with memory decay.PLoS Comput Biol. 2021 May 26;17(5):e1008995. doi: 10.1371/journal.pcbi.1008995. eCollection 2021 May. PLoS Comput Biol. 2021. PMID: 34038404 Free PMC article.
-
Measuring self-similarity in empirical signals to understand musical beat perception.Eur J Neurosci. 2025 Jan;61(2):e16637. doi: 10.1111/ejn.16637. Eur J Neurosci. 2025. PMID: 39853878 Free PMC article.
-
Humans can find rhythm in randomly timed sounds.R Soc Open Sci. 2025 Aug 20;12(8):250453. doi: 10.1098/rsos.250453. eCollection 2025 Aug. R Soc Open Sci. 2025. PMID: 40843187 Free PMC article.
-
Expectation adaptation for rare cadences in music: Item order matters in repetition priming.Cognition. 2023 Nov;240:105601. doi: 10.1016/j.cognition.2023.105601. Epub 2023 Aug 19. Cognition. 2023. PMID: 37604028 Free PMC article.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

