Drug sensitivity prediction with normal inverse Gaussian shrinkage informed by external data

Abstract

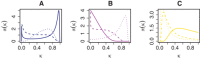
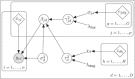
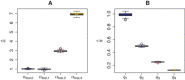
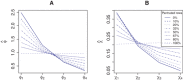
In precision medicine, a common problem is drug sensitivity prediction from cancer tissue cell lines. These types of problems entail modelling multivariate drug responses on high-dimensional molecular feature sets in typically >1000 cell lines. The dimensions of the problem require specialised models and estimation methods. In addition, external information on both the drugs and the features is often available. We propose to model the drug responses through a linear regression with shrinkage enforced through a normal inverse Gaussian prior. We let the prior depend on the external information, and estimate the model and external information dependence in an empirical-variational Bayes framework. We demonstrate the usefulness of this model in both a simulated setting and in the publicly available Genomics of Drug Sensitivity in Cancer data.

Keywords: Genomics of Drug Sensitivity in Cancer (GDSC); drug sensitivity; empirical Bayes; variational Bayes.

FIGURE 1

Implied prior densities $\pi ({\kappa }_{jd})$ for the (A) NIG, (B) Student's t, and (C) lasso priors. Different line types correspond to different hyperparameter settings. The hyperparameter settings (given in Section 3 of the SM) were chosen to show some possible, distinct shapes that each of the priors can take

FIGURE 2

Hierarchical representation of the drug sensitivity prediction model. Grey circles represent observed variables, white circles represent unobserved variables, tilted squares represent fixed data, and unenclosed letters are parameters to be estimated. Cell lines are indexed by i, features by j, drugs by d, drug covariates by h, and feature covariates by g. The $y_{id}$ are the drug sensitivities, $x_{ij}$ the molecular features, $c_{jdg}$ the external feature covariates, $z_{dh}$ the external drug covariates, ${\beta }_{jd}$ the regression coefficients, ${\sigma }_d^2$ the error variances, ${\tau }_d^2$ and ${\gamma }_{jd}^2$ the drug and feature specific variance components, respectively, and ${\varphi }_{jd}$, ${\lambda }_{\text{feat}}$, ${\chi }_d$, and ${\lambda }_{\text{drug}}$ the hyperparameters

FIGURE 3

Simulation results for Scenario 1 (${\tau }_d^2$ fixed): estimated and true values for (A) ${\alpha }_{\text{feat}}$ and (B) prior means ${\varphi }_{jd}$

FIGURE 4

Simulation results for Scenario 2 (${\gamma }_{jd}^2$ fixed): estimated (boxplots) and true values (triangles) for (A) ${\alpha }_{\text{feat}}$ and (B) prior means ${\varphi }_{jd}$

FIGURE 5

Simulation results for Scenario 3: estimated (boxplots) and true values (triangles) for (A) ${\alpha }_{\text{feat}}$, (B) prior means ${\varphi }_{jd}$, (C) ${\alpha }_{\text{drug}}$, and (D) prior means ${\chi }_d$

FIGURE 6

Simulation results for Scenario 3: mean estimated prior variances $\mathbb{V}({\beta }_{jd})$ versus true values, with line of identity (dotted)

FIGURE 7

Simulation results for Scenario 3: mean estimated prior means (A) ${\varphi }_{jd}$, and (B) ${\chi }_d$ for different levels of noise in the external covariates

FIGURE 8

Simulation results for Scenario 3: mean estimated prior Kurtoses $\mathcal{K}({\beta }_{jd})$ versus true values, with line of identity (dotted)