Neural mass modeling of slow-fast dynamics of seizure initiation and abortion
- PMID: 33166277
- PMCID: PMC7676664
- DOI: 10.1371/journal.pcbi.1008430
Neural mass modeling of slow-fast dynamics of seizure initiation and abortion
Abstract
Epilepsy is a dynamic and complex neurological disease affecting about 1% of the worldwide population, among which 30% of the patients are drug-resistant. Epilepsy is characterized by recurrent episodes of paroxysmal neural discharges (the so-called seizures), which manifest themselves through a large-amplitude rhythmic activity observed in depth-EEG recordings, in particular in local field potentials (LFPs). The signature characterizing the transition to seizures involves complex oscillatory patterns, which could serve as a marker to prevent seizure initiation by triggering appropriate therapeutic neurostimulation methods. To investigate such protocols, neurophysiological lumped-parameter models at the mesoscopic scale, namely neural mass models, are powerful tools that not only mimic the LFP signals but also give insights on the neural mechanisms related to different stages of seizures. Here, we analyze the multiple time-scale dynamics of a neural mass model and explain the underlying structure of the complex oscillations observed before seizure initiation. We investigate population-specific effects of the stimulation and the dependence of stimulation parameters on synaptic timescales. In particular, we show that intermediate stimulation frequencies (>20 Hz) can abort seizures if the timescale difference is pronounced. Those results have the potential in the design of therapeutic brain stimulation protocols based on the neurophysiological properties of tissue.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
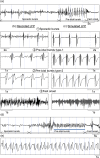

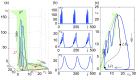
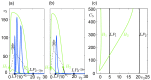
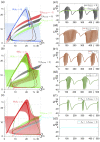
Similar articles
-
Preventive and Abortive Strategies for Stimulation Based Control of Epilepsy: A Computational Model Study.Int J Neural Syst. 2016 Dec;26(8):1650028. doi: 10.1142/S0129065716500283. Epub 2016 Apr 4. Int J Neural Syst. 2016. PMID: 27389003
-
Dual mechanisms of ictal high frequency oscillations in human rhythmic onset seizures.Sci Rep. 2020 Nov 5;10(1):19166. doi: 10.1038/s41598-020-76138-7. Sci Rep. 2020. PMID: 33154490 Free PMC article.
-
Neurostimulation stabilizes spiking neural networks by disrupting seizure-like oscillatory transitions.Sci Rep. 2020 Sep 21;10(1):15408. doi: 10.1038/s41598-020-72335-6. Sci Rep. 2020. PMID: 32958802 Free PMC article.
-
Modern concepts of seizure modeling.Int Rev Neurobiol. 2014;114:121-53. doi: 10.1016/B978-0-12-418693-4.00006-6. Int Rev Neurobiol. 2014. PMID: 25078501 Review.
-
Challenges for emerging neurostimulation-based therapies for real-time seizure control.Epilepsy Behav. 2011 Sep;22(1):118-25. doi: 10.1016/j.yebeh.2011.04.007. Epub 2011 Jun 12. Epilepsy Behav. 2011. PMID: 21664192 Review.
Cited by
-
Salidroside Attenuates Epilepsy and Cognitive Dysfunction in Rats by Downregulating Complement C3-C3aR Pathway-Mediated Activation of Microglia and Astrocytes.Neurochem Res. 2025 Aug 21;50(5):271. doi: 10.1007/s11064-025-04514-8. Neurochem Res. 2025. PMID: 40839226
-
Construction and Analysis of a New Resting-State Whole-Brain Network Model.Brain Sci. 2024 Feb 29;14(3):240. doi: 10.3390/brainsci14030240. Brain Sci. 2024. PMID: 38539628 Free PMC article.
-
Exploration of interictal to ictal transition in epileptic seizures using a neural mass model.Cogn Neurodyn. 2024 Jun;18(3):1215-1225. doi: 10.1007/s11571-023-09976-6. Epub 2023 May 16. Cogn Neurodyn. 2024. PMID: 38826671 Free PMC article.
-
Perturbations both trigger and delay seizures due to generic properties of slow-fast relaxation oscillators.PLoS Comput Biol. 2021 Mar 29;17(3):e1008521. doi: 10.1371/journal.pcbi.1008521. eCollection 2021 Mar. PLoS Comput Biol. 2021. PMID: 33780437 Free PMC article.
-
Development of Mechanistic Neural Mass (mNM) Models that Link Physiology to Mean-Field Dynamics.Front Netw Physiol. 2022 Sep;2:911090. doi: 10.3389/fnetp.2022.911090. Epub 2022 Sep 28. Front Netw Physiol. 2022. PMID: 36876035 Free PMC article.
References
-
- Dudek FE, Staley KJ. The Time Course and Circuit Mechanisms of Acquired Epileptogenesis. In: Noebels JL, Avoli M, Rogawski MA, Olsen RW, Delgado-Escueta AV, editors. Jasper’s Basic Mechanisms of the Epilepsies. 4th ed. Bethesda (MD): National Center for Biotechnology Information (US); 2012. - PubMed

