Independent components of human brain morphology
- PMID: 33186714
- PMCID: PMC7836233
- DOI: 10.1016/j.neuroimage.2020.117546
Independent components of human brain morphology
Abstract
Quantification of brain morphology has become an important cornerstone in understanding brain structure. Measures of cortical morphology such as thickness and surface area are frequently used to compare groups of subjects or characterise longitudinal changes. However, such measures are often treated as independent from each other. A recently described scaling law, derived from a statistical physics model of cortical folding, demonstrates that there is a tight covariance between three commonly used cortical morphology measures: cortical thickness, total surface area, and exposed surface area. We show that assuming the independence of cortical morphology measures can hide features and potentially lead to misinterpretations. Using the scaling law, we account for the covariance between cortical morphology measures and derive novel independent measures of cortical morphology. By applying these new measures, we show that new information can be gained; in our example we show that distinct morphological alterations underlie healthy ageing compared to temporal lobe epilepsy, even on the coarse level of a whole hemisphere. We thus provide a conceptual framework for characterising cortical morphology in a statistically valid and interpretable manner, based on theoretical reasoning about the shape of the cortex.
Copyright © 2020. Published by Elsevier Inc.
Figures
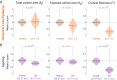

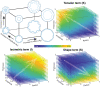

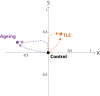
References
-
- Aljabar P., Wolz R., Srinivasan L., Counsell S.J., Rutherford M.A., Edwards A.D., Hajnal J.V., Rueckert D. A combined manifold learning analysis of shape and appearance to characterize neonatal brain development. IEEE Trans. Med. Imaging. 2011;30(12):2072–2086. doi: 10.1109/TMI.2011.2162529. - DOI - PubMed
-
- Carmon, J., Heege, J., Necus, J. H., Owen, T. W., Pipa, G., Kaiser, M., Taylor, P. N., Wang, Y., 2019. Reliability and comparability of human brain structural covariance networks. arXiv:1911.12755 [q-bio]ArXiv: 1911.12755. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

