Modelling of Phase Contrast Imaging with X-ray Wavefront Sensor and Partial Coherence Beams

Abstract

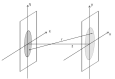
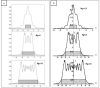
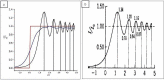
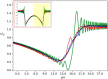
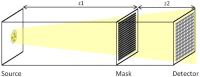
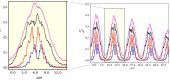
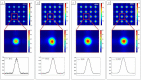
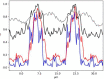
The Hartmann wavefront sensor is able to measure, separately and in absolute, the real δ and imaginary part β of the X-ray refractive index. While combined with tomographic setup, the Hartman sensor opens many interesting opportunities behind the direct measurement of the material density. In order to handle the different ways of using an X-ray wavefront sensor in imaging, we developed a 3D wave propagation model based on Fresnel propagator. The model can manage any degree of spatial coherence of the source, thus enabling us to model experiments accurately using tabletop, synchrotron or X-ray free-electron lasers. Beam divergence is described in a physical manner consistent with the spatial coherence. Since the Hartmann sensor can detect phase and absorption variation with high sensitivity, a precise simulation tool is thus needed to optimize the experimental parameters. Examples are displayed.

Keywords: Hartmann sensor; partial coherence; phase-contrast imaging; simulation.

Figure 1

Schematic representation of the coordinates system: the wave field is defined in the (ε,η) plane and propagated until the second plane (x,y). The propagation direction z is orthogonal to both planes.

Figure 2

Diffraction patterns from a rectangular aperture changing the Fresnel number (N_f). (a) Simulation results for N_f = 1, 4, 10; aperture size is shown in dark grey. (b) Theoretical results for N_f = 1, 4, 10; aperture size is shown in dark grey.

Figure 3

Diffraction pattern from a plane wave incident to a sharp edge in the case of coherent and incoherent illumination. (a) Result from the simulation for N = 5 (black line) and N = 100 (blue line). (b) Theoretical result for coherent illumination.

Figure 4

2D intensity map of a Polymethylmethacrylate (PMMA) cylinder normalized to the incident beam for different values of N: (a) N = 1, (b) N = 10, (c) N = 100 and (d) N = 1000. Diffraction lines can be seen in the case of full coherence (a). For higher N, the oscillations attenuate (b,c), while the image is smoothed for incoherent illumination (d). Scale bars are 25 µm.

Figure 5

Single line plot of the 2D images displayed in Figure 4. Green line (N = 1) represents the case of fully coherent illumination, while the red line is for N = 10, the blue for N = 100 and the black for N = 1000. The inset shows the full line plot.

Figure 6

Schematic representation of the simulated set-up: the Hartmann mask is placed in the beam path between the source and the detector. z₁ is the source to mask distance and z₂ is the mask to detector distance.

Figure 7

2D intensity maps of the simulated Hartmann mask imaged at the detector plane for different values of N. (a) N = 1, (b) N = 10, (c) N = 100 and (d) N = 1000. The diffraction pattern created with coherent illumination (a) will become more noisy increasing N, reaching a Gaussian shape in the incoherent case (d). Insets show a magnification of the central part of the mask. Scale bars are 16 µm.

Figure 8

Single line plot of the 2D images shown in Figure 7 varying N. N = 1 (blue line), N = 10 (red line), N = 100 (black line) and N = 1000 (purple line).

Figure 9

2D Intensity map of Hartmann mask with 3 µm square apertures and 25 µm pitches for different illuminating sources. The number of Gaussians N inside the source are N = 1 (a), N = 10 (b), N = 50 (c) and N = 1000 (d). Oscillations can be seen in the detected spots with coherent illumination (a) while they become quite circular in the incoherent case (d). Scale bars are 38 µm.

Figure 10

2D intensity map of the Hartmann mask at the Talbot plane increasing N. For N = 1 (a) the square pattern of the mask is exactly reproduced, while for N = 10 (b) and for N = 100 (c) the image is blurred. In the incoherent case N = 1000 (d) the square shape is completely lost. Insets show a magnification of the central part of the mask. Scale bars are 15 µm.

Figure 11

Single line plot of the images shown in Figure 9. N = 1 (blue line), N = 10 (red line), N = 100 (black line) and N = 1000 (gray line).