Dynamics of epidemics: Impact of easing restrictions and control of infection spread
- PMID: 33199943
- PMCID: PMC7657878
- DOI: 10.1016/j.chaos.2020.110431
Dynamics of epidemics: Impact of easing restrictions and control of infection spread
Abstract
During an infectious disease outbreak, mathematical models and computational simulations are essential tools to characterize the epidemic dynamics and aid in design public health policies. Using these tools, we provide an overview of the possible scenarios for the COVID-19 pandemic in the phase of easing restrictions used to reopen the economy and society. To investigate the dynamics of this outbreak, we consider a deterministic compartmental model (SEIR model) with an additional parameter to simulate the restrictions. In general, as a consequence of easing restrictions, we obtain scenarios characterized by high spikes of infections indicating significant acceleration of the spreading disease. Finally, we show how such undesirable scenarios could be avoided by a control strategy of successive partial easing restrictions, namely, we tailor a successive sequence of the additional parameter to prevent spikes in phases of low rate of transmissibility.
Keywords: COVID-19; Control of infection spread; Easing restrictions; SEIR model; Spikes of infections.
© 2020 Elsevier Ltd. All rights reserved.
Conflict of interest statement
We wish to confirm that there are no known conflicts of interest associated with this work and there has been no significant financial support for this work that could have influenced its outcome.
Figures
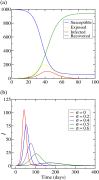







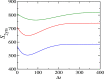

References
-
- McLean A., May R., Pattison J., Weiss R. OUP Oxford; 2005. SARS: a case study in emerging infections.
-
- Anderson R. 1st ed. Chapman & Hall; 1982. Population dynamics of infectious diseases.
-
- Anderson R.M., May R.M., Anderson B. Oxford University Press; 1992. Infectious diseases of humans: dynamics and control.
LinkOut - more resources
Full Text Sources
Other Literature Sources

