Unbalanced SSFP for super-resolution in MRI

Abstract

Purpose: To achieve rapid, low specific absorption rate (SAR) super-resolution imaging by exploiting the characteristic magnetization off-resonance profile in SSFP.

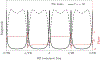
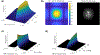
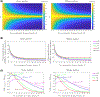
Theory and methods: In the presented technique, low flip angle unbalanced SSFP imaging is used to acquire a series of images at a low nominal resolution that are then combined in a super-resolution strategy analogous to non-linear structured illumination microscopy. This is demonstrated in principle via Bloch simulations and synthetic phantoms, and the performance is quantified in terms of point-spread function (PSF) and SNR for gray and white matter from field strengths of 0.35T to 9.4T. A k-space reconstruction approach is proposed to account for B₀ effects. This was applied to reconstruct super-resolution images from a test object at 9.4T.

Results: Artifact-free super-resolution images were produced after incorporating sufficient preparation time for the magnetization to approach the steady state. High-resolution images of a test object were obtained at 9.4T, in the presence of considerable B₀ inhomogeneity. For gray matter, the highest achievable resolution ranges from 3% of the acquired voxel dimension at 0.35T, to 9% at 9.4T. For white matter, this corresponds to 3% and 10%, respectively. Compared to an equivalent segmented gradient echo acquisition at the optimal flip angle, with a fixed TR of 8 ms, gray matter has up to 34% of the SNR at 9.4T while using a ×10 smaller flip angle. For white matter, this corresponds to 29% with a ×11 smaller flip angle.

Conclusion: This approach achieves high degrees of super-resolution enhancement with minimal RF power requirements.

Keywords: SSFP; spatial encoding; structured illumination microscopy; super-resolution.

FIGURE 1

Magnitude of the Bloch-simulated off-resonance profile for a tissue with T₁ = 600 ms and T₂ = 100 ms, in a bSSFP acquisition at flip angles of 1° (solid black line) and 30° (dashed black line), with TR = 5 ms. The corresponding phase profile is overlaid in red

FIGURE 2

(A) Sequence diagram for the proposed technique, which uses an additional unbalanced spoiler gradient in 1 direction (shaded black). Here, the spoiler gradient is used in the phase encoding direction, but it can be applied along any axis. (B) Schematic of the intravoxel signal modulation during the experiment. Over a series of N images, the modulation pattern is swept across the voxel in regular increments. These can then be stitched together to create a super-resolution image

FIGURE 3

Off-resonance profiles of gray matter at 3T with a 1° flip angle, and corresponding Fourier transforms when this is repeated along a spatial dimension: (A) with the RF phase cycling increment equal to zero; (B) with non-zero linear phase cycling increment; (C) using the magnitude of the off-resonance profile of (A); (D) using the magnitude of the off-resonance profile of (B). Note the marked asymmetry in the k-space harmonics in (A) and (B). Also note the sinusoidal modulation of the harmonics in (B) and (D)

FIGURE 4

Illustration of the multi-frequency reconstruction procedure. A phase offset it is introduced to Ψ to mimic a local offset frequency ω, and a low-pass image (Im_LP) is obtained by zero-filling a single band of k-space data (S_LP) and performing the inverse Fourier transform. The phase of this image is calculated, and the process repeated for a range of offset frequencies. A map of ω is obtained by finding the value that minimizes the absolute phase on a voxel-wise basis. Finally, full-resolution images are reconstructed at each of the same offset frequencies, and the reconstruction at the optimal ω is chosen on a voxel-wise basis

FIGURE 5

(A) Flip angle dependence of the bSSFP signal profile, for tissue parameters of T₁= 600 ms and T₂= 100 ms, and TR = 5 ms. (B) Bloch simulation of COMBINE in a numeric brain phantom, in the presence of spatial ${\text{B}}_1^{+}$ in homogeneity. (C) T₁ dependence of the bSSFP signal profile, for a flip angle of 1°, TR = 5 ms, and T₂= 100 ms. (D) T₂dependence of the bSSFP signal profile, for a flip angle of 1°, TR = 5 ms, and T₁ = 600 ms

FIGURE 6

Illustration of the efficiency considerations when comparing the approach to traditional GRE sequence with the same TR of 5 ms. Left: the GRE signal is assumed to be perfectly spoiled so that the magnitude in each voxel (with nominal voxel size Δ_ynom ≡ Δ_y) is the mean of the bSSFP profile at 30°, and results in a total acquisition time of TA_Trad. Right: illustration of the proposed approach with a resolution enhancement factor of 20, determined by the FWHM of the off-resonance profile. In this case, the nominal voxel size (Δy_nom) is 20 times larger than the desired super-resolution voxel size (Δy₎, and each image is acquired 20 times faster. The full image is acquired in the same total time (because TR is equal), and the integral of the magnitude signal in the final image is near equivalency, but there is an SNR efficiency penalty of approximately $\sqrt{20}$

FIGURE 7

(A) Bloch simulated k-space weighting for gray matter (left) and white matter (right) with a flip angle of 1°, using T₁ and T₂ from Zhu et al, and with increasing M. (B) Bloch simulated point-spread function for gray matter (left) and white matter (right) at different field strengths with a flip angle of 1°, using T₁ and T₂ from Zhu et al, and in comparison to the ideal voxel size. (C) SNR of COMBINE with a flip angle of 1° in comparison to a partial-Fourier gradient spoiledM-segment acquisition at the optimal flip angle and TE = 0, for T₁ and T₂of gray and white matter observed at different field strengths. Both acquisitions use the same arbitrary TR of 8 ms, and record the same number of k-space lines. This excludes any aliasing effects during the COMBINE reconstruction

FIGURE 8

Bloch simulations on a numeric brain phantom, applying the proposed super-resolution approach to generate a 289 × 289 image from 17 low-resolution 17 × 289 images. As the number of dummy TRs are increased from left to right, the reconstruction artefacts decrease

FIGURE 9

(A) Demonstration of the super-resolution approach in the physical phantom, including (from left–right): the mean of the low-resolution input images; single frequency super-resolution reconstruction; multifrequency super-resolution reconstruction; vendor-provided B₀ map (that was not used in the reconstruction but is provided for reference) indicating the presence of substantial static field inhomogeneities. 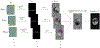(B) Close-up of the images obtained from the physical phantom, including (from left–right): a reference structural scout image; the mean of the low-resolution input images; a bicubic interpolation of the mean of the low-resolution input images; and the proposed multifrequency super-resolution reconstruction. The proposed approach clearly enhances spatial resolution in comparison to straightforward image interpolation

FIGURE 10

(A) Reconstructions at a single frequency from different combinations of M and N from a COMBINE acquisition of 36 images at equidistant phase cycling offsets. Each reconstruction produces a matrix size that is 2M-1 times larger along the super-resolution dimension. (B) For the same number of input images (N= 36), increasing M improves the spatial resolution of the resultant image and reduces the SNR. For large M, the additional reconstructed k-space bands contribute more noise than useful high-resolution information. (C) The difference of 2 acquisitions with the same M but different N (N= M= 1; M= 1, N= 36). The subtraction image shows that aliasing produces structured variance, localized to regions where there is a significant local B₀ offset because of eg, air bubbles. Outside of these regions the aliasing effects are benign