SINDy-PI: a robust algorithm for parallel implicit sparse identification of nonlinear dynamics

Abstract

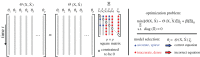
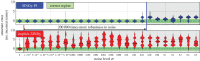
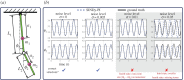
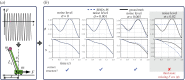
Accurately modelling the nonlinear dynamics of a system from measurement data is a challenging yet vital topic. The sparse identification of nonlinear dynamics (SINDy) algorithm is one approach to discover dynamical systems models from data. Although extensions have been developed to identify implicit dynamics, or dynamics described by rational functions, these extensions are extremely sensitive to noise. In this work, we develop SINDy-PI (parallel, implicit), a robust variant of the SINDy algorithm to identify implicit dynamics and rational nonlinearities. The SINDy-PI framework includes multiple optimization algorithms and a principled approach to model selection. We demonstrate the ability of this algorithm to learn implicit ordinary and partial differential equations and conservation laws from limited and noisy data. In particular, we show that the proposed approach is several orders of magnitude more noise robust than previous approaches, and may be used to identify a class of ODE and PDE dynamics that were previously unattainable with SINDy, including for the double pendulum dynamics and simplified model for the Belousov-Zhabotinsky (BZ) reaction.

Keywords: model selection; optimization; rational differential equations; system identification.

Figure 1.

The illustration of the SINDy-PI algorithm on Michaelis–Menten dynamics. (a) The Michaelis–Menten system is simulated, and measurement data is provided to SINDy-PI. (b) Multiple possible left-hand side functions are tested at the same time. (c) The candidate model prediction error is calculated, and the best model is selected. (Online version in colour.)

Figure 2.

Schematic illustrating the constrained formulation of the SINDy-PI algorithm. (Online version in colour.)

Figure 3.

SINDy-PI and implicit-SINDy are compared on the Michaelis–Menten kinetics, where the structure error quantifies the number of terms in the model that are incorrectly added or deleted, compared with the true model. The derivative is computed by the total-variation regularization difference (TVRegDiff) [56] on noisy state measurements. The violin plots show the cross-validated distribution of the number of incorrect terms across 30 models. The green region (a rectangle stripe at zero value labelled as correct region) indicates no structural difference between the identified model and the ground truth model. Details are provided in appendix A(b). (Online version in colour.)

Figure 4.

Success rate of SINDy-PI and implicit-SINDy identifying yeast glycolysis (3.10f) with different percentage of training data. Each data usage percentage is randomly sampled from the entire dataset composed of all trajectories. The success rate is calculated by averaging the results of 20 runs. (Online version in colour.)

Figure 5.

Comparison of SINDy-PI and PDE-FIND on an implicit PDE problem given by the modified KdV equation (3.11). As we increase g₀, the rational term begins to play a significant role in the system behaviour. For small g₀, PDE-FIND compensates for the effect of the rational term by tuning the other coefficients. When g₀ is large, PDE-FIND overfits the library. SINDy-PI, on the other hand, correctly identifies the rational term. (Online version in colour.)

Figure 6.

Schematic illustration of SINDy-PI identifying a mounted double pendulum system. (a) Data generation; (b) SINDy-PI Identified Model Performance. (Online version in colour.)

Figure 7.

SINDy-PI is used to identify the single pendulum on a cart system. Control is applied to the cart, and both the cart and pendulum states are measured. When the measurement noise is small, SINDy-PI can identify the correct structure of the model. (a) Data generation; (b) SINDy-PI identified model performance. (Online version in colour.)

Figure 8.

SINDy-PI is able to identify the simplified Belousov–Zhabotinsky reaction model. (Online version in colour.)

Figure 9.

SINDy-PI is used to extract the conserved quantity for a double pendulum. (Online version in colour.)

Figure 10.

Comparison of the model identified by SINDy, Implicit-SINDy, and SINDy-PI on Michaelis–Menten dynamics. (a) Both SINDy-PI and Implicit-SINDy identified the correct model. However, the SINDy model only agrees for x near the origin. (b–d) As Gaussian noise level increases, the SINDy model degrades further. (Online version in colour.)