A Guide to Fluorescence Lifetime Microscopy and Förster's Resonance Energy Transfer in Neuroscience
- PMID: 33232577
- PMCID: PMC8274369
- DOI: 10.1002/cpns.108
A Guide to Fluorescence Lifetime Microscopy and Förster's Resonance Energy Transfer in Neuroscience
Abstract
Fluorescence lifetime microscopy (FLIM) and Förster's resonance energy transfer (FRET) are advanced optical tools that neuroscientists can employ to interrogate the structure and function of complex biological systems in vitro and in vivo using light. In neurobiology they are primarily used to study protein-protein interactions, to study conformational changes in protein complexes, and to monitor genetically encoded FRET-based biosensors. These methods are ideally suited to optically monitor changes in neurons that are triggered optogenetically. Utilization of this technique by neuroscientists has been limited, since a broad understanding of FLIM and FRET requires familiarity with the interactions of light and matter on a quantum mechanical level, and because the ultra-fast instrumentation used to measure fluorescent lifetimes and resonance energy transfer are more at home in a physics lab than in a biology lab. In this overview, we aim to help neuroscientists overcome these obstacles and thus feel more comfortable with the FLIM-FRET method. Our goal is to aid researchers in the neuroscience community to achieve a better understanding of the fundamentals of FLIM-FRET and encourage them to fully leverage its powerful ability as a research tool. Published 2020. U.S. Government.
Keywords: FLIM; FRET; FRET-based biosensor; conformational change; fiber-photometry; microscopy; protein-protein interaction.
Published 2020. This article is a US Government work and is in the public domain in the USA.
Figures
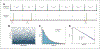





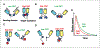
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

