Gradient waveform design for tensor-valued encoding in diffusion MRI
- PMID: 33242529
- PMCID: PMC8443151
- DOI: 10.1016/j.jneumeth.2020.109007
Gradient waveform design for tensor-valued encoding in diffusion MRI
Abstract
Diffusion encoding along multiple spatial directions per signal acquisition can be described in terms of a b-tensor. The benefit of tensor-valued diffusion encoding is that it unlocks the 'shape of the b-tensor' as a new encoding dimension. By modulating the b-tensor shape, we can control the sensitivity to microscopic diffusion anisotropy which can be used as a contrast mechanism; a feature that is inaccessible by conventional diffusion encoding. Since imaging methods based on tensor-valued diffusion encoding are finding an increasing number of applications we are prompted to highlight the challenge of designing the optimal gradient waveforms for any given application. In this review, we first establish the basic design objectives in creating field gradient waveforms for tensor-valued diffusion MRI. We also survey additional design considerations related to limitations imposed by hardware and physiology, potential confounding effects that cannot be captured by the b-tensor, and artifacts related to the diffusion encoding waveform. Throughout, we discuss the expected compromises and tradeoffs with an aim to establish a more complete understanding of gradient waveform design and its impact on accurate measurements and interpretations of data.
Keywords: Diffusion magnetic resonance imaging; Gradient waveform design; Tensor-valued diffusion encoding.
Copyright © 2020 The Author(s). Published by Elsevier B.V. All rights reserved.
Figures





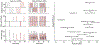


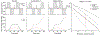
References
-
- Afzali M, Tax CMW, Chatziantoniou C, Jones DK, 2019. Comparison of different tensor encoding combinations in microstructural parameter estimation. 2019 Ieee 16th International Symposium on Biomedical Imaging (Isbi 2019)1471–1474.
-
- Ahn CB, Lee SY, Nalcioglu O, Cho ZH, 1987. The effects of random directional distributed flow in nuclear magnetic resonance imaging. Med. Phys 14, 43–48. - PubMed
-
- Alexander DC, 2009. Modelling, Fitting and Sampling in Diffusion MRI. Visualization and Processing of Tensor Fields. Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 3–20.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

