Fractional SIR epidemiological models
- PMID: 33257790
- PMCID: PMC7705759
- DOI: 10.1038/s41598-020-77849-7
Fractional SIR epidemiological models
Abstract
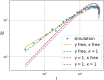
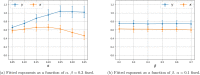
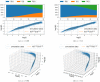
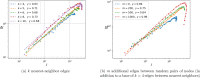
The purpose of this work is to make a case for epidemiological models with fractional exponent in the contribution of sub-populations to the incidence rate. More specifically, we question the standard assumption in the literature on epidemiological models, where the incidence rate dictating propagation of infections is taken to be proportional to the product between the infected and susceptible sub-populations; a model that relies on strong mixing between the two groups and widespread contact between members of the groups. We contend, that contact between infected and susceptible individuals, especially during the early phases of an epidemic, takes place over a (possibly diffused) boundary between the respective sub-populations. As a result, the rate of transmission depends on the product of fractional powers instead. The intuition relies on the fact that infection grows in geographically concentrated cells, in contrast to the standard product model that relies on complete mixing of the susceptible to infected sub-populations. We validate the hypothesis of fractional exponents (1) by numerical simulation for disease propagation in graphs imposing a local structure to allowed disease transmissions and (2) by fitting the model to the JHU CSSE COVID-19 Data for the period Jan-22-20 to April-30-20, for the countries of Italy, Germany, France, and Spain.
Conflict of interest statement
The authors declare no competing interests.
Figures

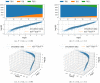
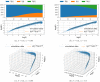
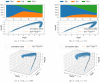
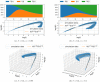
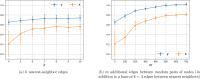
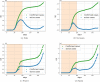
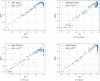
Update of
-
Fractional SIR Epidemiological Models.medRxiv [Preprint]. 2020 Apr 30:2020.04.28.20083865. doi: 10.1101/2020.04.28.20083865. medRxiv. 2020. Update in: Sci Rep. 2020 Nov 30;10(1):20882. doi: 10.1038/s41598-020-77849-7. PMID: 32511496 Free PMC article. Updated. Preprint.
Similar articles
-
Fractional SIR Epidemiological Models.medRxiv [Preprint]. 2020 Apr 30:2020.04.28.20083865. doi: 10.1101/2020.04.28.20083865. medRxiv. 2020. Update in: Sci Rep. 2020 Nov 30;10(1):20882. doi: 10.1038/s41598-020-77849-7. PMID: 32511496 Free PMC article. Updated. Preprint.
-
TW-SIR: time-window based SIR for COVID-19 forecasts.Sci Rep. 2020 Dec 31;10(1):22454. doi: 10.1038/s41598-020-80007-8. Sci Rep. 2020. PMID: 33384444 Free PMC article.
-
Modelling the initial epidemic trends of COVID-19 in Italy, Spain, Germany, and France.PLoS One. 2020 Nov 9;15(11):e0241743. doi: 10.1371/journal.pone.0241743. eCollection 2020. PLoS One. 2020. PMID: 33166344 Free PMC article.
-
Is Lockdown Effective in Limiting SARS-CoV-2 Epidemic Progression?-a Cross-Country Comparative Evaluation Using Epidemiokinetic Tools.J Gen Intern Med. 2021 Mar;36(3):746-752. doi: 10.1007/s11606-020-06345-5. Epub 2021 Jan 13. J Gen Intern Med. 2021. PMID: 33442818 Free PMC article.
-
'Dark matter', second waves and epidemiological modelling.BMJ Glob Health. 2020 Dec;5(12):e003978. doi: 10.1136/bmjgh-2020-003978. BMJ Glob Health. 2020. PMID: 33328201 Free PMC article. Review.
Cited by
-
An SIR-type epidemiological model that integrates social distancing as a dynamic law based on point prevalence and socio-behavioral factors.Sci Rep. 2021 May 13;11(1):10170. doi: 10.1038/s41598-021-89492-x. Sci Rep. 2021. PMID: 33986347 Free PMC article.
-
Effects of human mobility and behavior on disease transmission in a COVID-19 mathematical model.Sci Rep. 2022 Jun 27;12(1):10840. doi: 10.1038/s41598-022-14155-4. Sci Rep. 2022. PMID: 35760930 Free PMC article.
-
Mask or no mask for COVID-19: A public health and market study.PLoS One. 2020 Aug 14;15(8):e0237691. doi: 10.1371/journal.pone.0237691. eCollection 2020. PLoS One. 2020. PMID: 32797067 Free PMC article.
-
Theoretical and numerical analysis of COVID-19 pandemic model with non-local and non-singular kernels.Sci Rep. 2022 Oct 28;12(1):18178. doi: 10.1038/s41598-022-21372-4. Sci Rep. 2022. PMID: 36307434 Free PMC article.
-
Exploring COVID-19 Daily Records of Diagnosed Cases and Fatalities Based on Simple Nonparametric Methods.Infect Dis Rep. 2021 Apr 1;13(2):302-328. doi: 10.3390/idr13020031. Infect Dis Rep. 2021. PMID: 33915940 Free PMC article.
References
-
- Bauer F, Castillo-Chavez C, Feng Z. Mathematical Models in Epidemiology. Berlin: Springer; 2019.
-
- Bjørnstad ON, Shea K, Krzywinski M, Altman N. Modeling infectious epidemics. Nat. Methods. 2020;20:20. - PubMed
-
- Capasso V. Mathematical Structures of Epidemic Systems. Berlin: Springer; 2008.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Research Materials
Miscellaneous

