Ingredients for robustness

Abstract

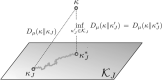
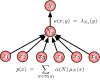
A core property of robust systems is given by the invariance of their function against the removal of some of their structural components. This intuition has been formalised in the context of input-output maps, thereby introducing the notion of exclusion independence. We review work on how this formalisation allows us to derive characterisation theorems that provide a basis for the design of robust systems.

Keywords: Interaction order; Knockouts; Neutrality; Robustness.

Fig. 1

An input–output map for the study of robustness

Fig. 2

Left: unperturbed function. Middle: knockout of node 3. Right: knockout of nodes 2 and 6

Fig. 3

Optimal function after knockout

Fig. 4

a A set $\mathcal{S}$ in ${\mathcal{X}}_I$; b the connected components of $\mathcal{S}$; c neutrality of the map on the connected components, indicated by colour

Fig. 5

Structure of a robust map

Fig. 6

Decomposition of the affinity

Fig. 7

Removal of the interaction terms ${\varphi }_{\{1,2,3\}}(x_1,x_2,x_3;y)$ and ${\varphi }_{\{3,4\}}(x_3,x_4;y)$ as result of the knockout of node 3