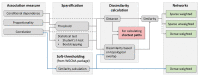
NetCoMi: network construction and comparison for microbiome data in R
- PMID: 33264391
- PMCID: PMC8293835
- DOI: 10.1093/bib/bbaa290
NetCoMi: network construction and comparison for microbiome data in R
Abstract
Motivation: Estimating microbial association networks from high-throughput sequencing data is a common exploratory data analysis approach aiming at understanding the complex interplay of microbial communities in their natural habitat. Statistical network estimation workflows comprise several analysis steps, including methods for zero handling, data normalization and computing microbial associations. Since microbial interactions are likely to change between conditions, e.g. between healthy individuals and patients, identifying network differences between groups is often an integral secondary analysis step. Thus far, however, no unifying computational tool is available that facilitates the whole analysis workflow of constructing, analysing and comparing microbial association networks from high-throughput sequencing data.
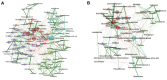
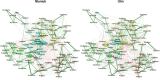
Results: Here, we introduce NetCoMi (Network Construction and comparison for Microbiome data), an R package that integrates existing methods for each analysis step in a single reproducible computational workflow. The package offers functionality for constructing and analysing single microbial association networks as well as quantifying network differences. This enables insights into whether single taxa, groups of taxa or the overall network structure change between groups. NetCoMi also contains functionality for constructing differential networks, thus allowing to assess whether single pairs of taxa are differentially associated between two groups. Furthermore, NetCoMi facilitates the construction and analysis of dissimilarity networks of microbiome samples, enabling a high-level graphical summary of the heterogeneity of an entire microbiome sample collection. We illustrate NetCoMi's wide applicability using data sets from the GABRIELA study to compare microbial associations in settled dust from children's rooms between samples from two study centers (Ulm and Munich).
Availability: R scripts used for producing the examples shown in this manuscript are provided as supplementary data. The NetCoMi package, together with a tutorial, is available at https://github.com/stefpeschel/NetCoMi.
Contact: Tel:+49 89 3187 43258; stefanie.peschel@mail.de.
Supplementary information: Supplementary data are available at Briefings in Bioinformatics online.
Keywords: compositional data; differential association; microbial association estimation; network analysis; network comparison; sample similarity network.
© The Author(s) 2020. Published by Oxford University Press.
Figures


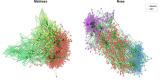
References
-
- Davidson RM, Epperson LE. Microbiome Sequencing Methods for Studying Human Diseases. In: Methods in Molecular Biology, Vol. 1706. Humana Press Inc., 2018, 77–90. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

