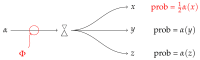
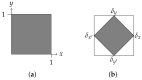
A Royal Road to Quantum Theory (or Thereabouts)

Abstract

This paper fails to derive quantum mechanics from a few simple postulates. However, it gets very close, and does so without much exertion. More precisely, I obtain a representation of finite-dimensional probabilistic systems in terms of Euclidean Jordan algebras, in a strikingly easy way, from simple assumptions. This provides a framework within which real, complex and quaternionic QM can play happily together and allows some (but not too much) room for more exotic alternatives. (This is a leisurely summary, based on recent lectures, of material from the papers arXiv:1206:2897 and arXiv:1507.06278, the latter joint work with Howard Barnum and Matthew Graydon. Some further ideas are also explored, developing the connection between conjugate systems and the possibility of forming stable measurement records and making connections between this approach and the categorical approach to quantum theory.).

Keywords: Jordan algebras; conjugate systems; reconstruction of quantum mechanics.

Figure 1

$\mathsf{\Phi }$ attenuates x’s sensitivity by $1/2$.

Figure 2

The state spaces of two bits. (a) The square bit; (b) The diamond bit.

Figure 3

(a) Two outcome-effects for the square bit; (b) An effect for the diamond bit not positive on the square bit.