Using the Data Agreement Criterion to Rank Experts' Beliefs

Abstract

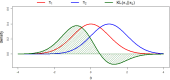
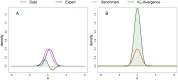
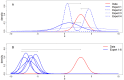
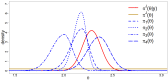
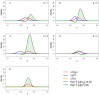
Experts' beliefs embody a present state of knowledge. It is desirable to take this knowledge into account when making decisions. However, ranking experts based on the merit of their beliefs is a difficult task. In this paper, we show how experts can be ranked based on their knowledge and their level of (un)certainty. By letting experts specify their knowledge in the form of a probability distribution, we can assess how accurately they can predict new data, and how appropriate their level of (un)certainty is. The expert's specified probability distribution can be seen as a prior in a Bayesian statistical setting. We evaluate these priors by extending an existing prior-data (dis)agreement measure, the Data Agreement Criterion, and compare this approach to using Bayes factors to assess prior specification. We compare experts with each other and the data to evaluate their appropriateness. Using this method, new research questions can be asked and answered, for instance: Which expert predicts the new data best? Is there agreement between my experts and the data? Which experts' representation is more valid or useful? Can we reach convergence between expert judgement and data? We provided an empirical example ranking (regional) directors of a large financial institution based on their predictions of turnover.

Keywords: Bayes; Bayes factor; Kullback–Leibler divergence; decision making; expert judgement; prior-data (dis)agreement; ranking.

Figure 1

KL divergences between two normal distributions. In this example, ${\mathsf{\pi }}_1$ is a standard normal distribution and ${\mathsf{\pi }}_2$ is a normal distribution with a mean of 1 and a variance of 1. The value of the KL divergence is equal to the integral over the parameter space for the function. The green shaded area above the x-axis adds to the KL divergence and the green shaded area below the x-axis subtracts from the KL divergence.

Figure 2

Calculating the DAC. In this example, ${\mathsf{\pi }}^{\mathrm{J}}\left(\mathsf{\theta }|y\right)$ is a standard normal distribution, $\mathsf{\pi }\left(\mathsf{\theta }\right)$ is a normal distribution with a mean of 0.5 and a variance of 1 and ${\mathsf{\pi }}^{\mathrm{J}}\left(\mathsf{\theta }\right)$ is a normal distribution with a mean of 0 and a variance of 900. The DAC < 1, thus prior-data agreement is concluded.

Figure 3

Scenarios in which there are multiple experts and one source of data. (A) shows experts differing in prediction and (un)certainty, all (dis)agreeing to a certain extent with the data; (B) shows a scenario in which all experts disagree with the data, which results in the question of which of the sources of information is correct.

Figure 4

The effect on the behavior of the ${\mathrm{DAC}}_{\mathrm{d}}$ for different choices for benchmark priors. All panels use the same data (N = 100) from a standard normal distribution and the same variations for ${\mathsf{\pi }}_{\mathrm{d}}\left(\mathsf{\theta }\right)$ which are the normal distribution for which the parameters for the mean and standard deviation are given on the x-axis and y-axis of the panels. In (A), the benchmark is the $N\left(0,10,000\right)$ density; in (B), the $N\left(0,1\right)$ density; in (C), the $U\left(-50,50\right)$ density and in (D), the $N\left(5,0.5\right)$ density.

Figure 5

Visual presentation of all relevant distributions for the empirical study; ${\mathsf{\pi }}_{\mathrm{d}}\left(\mathsf{\theta }\right)$, ${\mathsf{\pi }}^{\mathrm{J}}\left(\mathsf{\theta }\right)$ and ${\mathsf{\pi }}^{\mathrm{J}}(\mathsf{\theta }|y)$.

Figure 6

All KL divergences for ${\mathsf{\pi }}_{\mathrm{d}}\left(\mathsf{\theta }\right)$ (A–D) and ${\mathsf{\pi }}^{\mathrm{J}}\left(\mathsf{\theta }\right)$ (E) with ${\mathsf{\pi }}^{\mathrm{J}}(\mathsf{\theta }|y)$ as the distribution that is to be approximated. (A) is for expert one; (B) for expert two; (C) for expert three and (D) for expert four.