Non-Equilibrium Thermodynamics and Stochastic Dynamics of a Bistable Catalytic Surface Reaction

Abstract

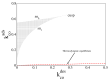
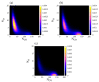
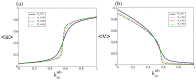
Catalytic surface reaction networks exhibit nonlinear dissipative phenomena, such as bistability. Macroscopic rate law descriptions predict that the reaction system resides on one of the two steady-state branches of the bistable region for an indefinite period of time. However, the smaller the catalytic surface, the greater the influence of coverage fluctuations, given that their amplitude normally scales as the square root of the system size. Thus, one can observe fluctuation-induced transitions between the steady-states. In this work, a model for the bistable catalytic CO oxidation on small surfaces is studied. After a brief introduction of the average stochastic modelling framework and its corresponding deterministic limit, we discuss the non-equilibrium conditions necessary for bistability. The entropy production rate, an important thermodynamic quantity measuring dissipation in a system, is compared across the two approaches. We conclude that, in our catalytic model, the most favorable non-equilibrium steady state is not necessary the state with the maximum or minimum entropy production rate.

Keywords: bistability; chemical master equation; entropy production rate; fluctuations; non-equilibrium steady state.

Figure 1

Steady state bifurcation diagram in the parameter space ($k_{co}^{ads}$, $k_{co}^{des}$) from Equations (19) and (20). Inside black region the system exhibits the bistable phenomenon. Its boundaries are given by the upper saddle node ($s{n}_h$) line and the lower saddle node ($s{n}_l$) line meeting each other in a cusp. Along the dashed-red line ($k_{co}^{ads}\approx 0.05k_{co}^{des}$), the system relaxes to thermodynamic equilibrium. Other parameters are $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice).

Figure 2

(a) and (b) Steady state bifurcation diagrams of the CO and oxygen coverages as a function of $k_{co}^{ads}$, for $k_{co}^{des}=0.15$. The figures clearly show a bistable region in which two NESS stable branches (blue lines) coexist with an unstable or saddle one (red dots). In all cases, the boundaries of the bistable region are characterised by saddle node bifurcations at the $s{n}_l$ and $s{n}_h$ points. Other parameters are $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice)

Figure 3

Time evolution of the system inside the bistable region and on the plane (u, $\nu$), for two different initial conditions. In this case, $k_{co}^{ads}=0.57$ and $k_{co}^{des}=0.15$. Depending on the initial condition, the system converges to one of the two NESS branches of the bistable region. Other parameters are $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice)

Figure 4

(a) Macroscopic entropy production rate, $EP$ (Equation (22)), corresponding to the steady-state solutions of Equations (19) and (20) as a function of $k_{co}^{ads}$, for $k_{co}^{des}=0.15$. (b) The same $EP$ but only for values of $k_{co}^{ads}$ around the bistable region. Full blue lines are the $EP$ associated with the ($u_{-}$, ${\nu }_{+}$) and ($u_{+}$, ${\nu }_{-}$) stable branches and dotted line to the one of the unstable or saddle branch or ($u_{saddle}$, ${\nu }_{saddle}$). Other parameters are $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice).

Figure 5

Time series of CO coverage from the deterministic and stochastic approaches. Blue dashed lines correspond to the deterministic prediction and full black lines to the stochastic one. (a) Stochastic simulations for a surface area of $N_L=1500$. Note as the stochastic trajectories follow on average the trajectories predicted by the deterministic approach; (b) Stochastic simulations with a surface area of $N_L=100$. Note the phenomenon of fluctuation-induced transitions. Other parameters are $k_{co}^{ads}=0.57$, $k_{co}^{des}=0.15$, $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice).

Figure 6

Normalised steady state probability distribution, $P_{st}\left(\mathbf{Z}\right)$, of finding a population vector $\mathbf{Z}=\{N_{CO},N_O\}$, for $N_L=200$. (a) $k_{co}^{ads}=0.55$; (b) $k_{co}^{ads}=0.56$; (c) $k_{co}^{ads}=0.57$. Other parameters are $k_{co}^{des}=0.15$, $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice). The steady state probability distribution was obtained after averaging over an ensemble (20 independent realisations sampled at a fixed time).

Figure 7

(a) and (b) Steady state bifurcation diagrams of the average CO and oxygen coverages as a function of $k_{co}^{ads}$, for $k_{co}^{des}=0.15$. Other parameters are $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice). The steady state probability distribution was obtained after averaging over an ensemble (20 independent realisations sampled at a fixed time). This figure should be compared with Figure 2.

Figure 8

(a) Stochastic entropy production rate measured as $N_L^{-1}d{S}_i/dt$ versus $k_{co}^{ads}$ for three different system sizes, and $k_{co}^{des}=0.15$; (b) The same as in (a) but only for values of $k_{co}^{ads}$ around the bistable region. Other parameters are $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice). To calculate this entropy production rate, the steady state probability distribution was obtained after averaging over an ensemble (20 independent realisations sampled at a fixed time). This figure should be compared with Figure 4.

Figure 9

(a) Deterministic overall CO₂ production rate; (b) Stochastic overall CO₂ production rate at stationary state. In both cases, $k_{co}^{ads}$ was variated and $k_{co}^{des}$ was fixed at $0.15$. Other parameters are $k_{o_2}^{ads}=0.2$, $k_o^{des}=20$, $k_{c{o}_2}=0.5$, $k_r=50$, and $\zeta =4$ (square lattice).