A Programmable Mechanical Maxwell's Demon
- PMID: 33266781
- PMCID: PMC7514173
- DOI: 10.3390/e21010065
A Programmable Mechanical Maxwell's Demon
Abstract
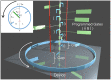
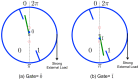
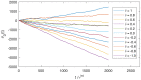
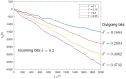
We introduce and investigate a simple and explicitly mechanical model of Maxwell's demon-a device that interacts with a memory register (a stream of bits), a thermal reservoir (an ideal gas) and a work reservoir (a mass that can be lifted or lowered). Our device is similar to one that we have briefly described elsewhere, but it has the additional feature that it can be programmed to recognize a chosen reference sequence, for instance, the binary representation of π . If the bits in the memory register match those of the reference sequence, then the device extracts heat from the thermal reservoir and converts it into work to lift a small mass. Conversely, the device can operate as a generalized Landauer's eraser (or copier), harnessing the energy of a dropping mass to write the chosen reference sequence onto the memory register, replacing whatever information may previously have been stored there. Our model can be interpreted either as a machine that autonomously performs a conversion between information and energy, or else as a feedback-controlled device that is operated by an external agent. We derive generalized second laws of thermodynamics for both pictures. We illustrate our model with numerical simulations, as well as analytical calculations in a particular, exactly solvable limit.
Keywords: Landauer’s principle; Maxwell’s demon; Shannon entropy; Szilard engine; information engine; second law of thermodynamics.
Conflict of interest statement
The authors declare no conflict of interest.
Figures




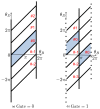
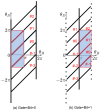

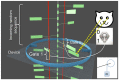
References
-
- Maxwell J.C. The Scientific Letters and Papers of James Clerk Maxwell. Volume 2. Cambridge University Press; Cambridge, UK: 1995. pp. 1862–1873.
-
- Smoluchowski M. Experimentell nachweisbare, der üblichen Thermodynamik widersprechende Molekularphänomene [Experimentally verifiable phenomena of molecules contradicting usual thermodynamics] Physikalische Zeitschrift. 1912;13:1069–1080. (In German)
-
- Feynman R.P., Leighton R.B., Sands M. The Feynman Lectures on Physics. Addison-Wesley; Reading, MA, USA: 1966.
-
- Landauer R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961;5:183–191. doi: 10.1147/rd.53.0183. - DOI
-
- Penrose O. Foundations of Statistical Mechanics. Volume 42 Pergamon Press; Oxford, UK: 1970.
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

