Centroid-Based Clustering with αβ-Divergences
- PMID: 33266911
- PMCID: PMC7514678
- DOI: 10.3390/e21020196
Centroid-Based Clustering with αβ-Divergences
Abstract
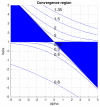
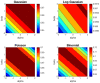
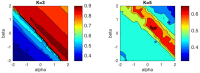
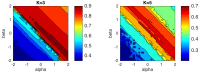
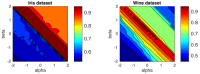
Centroid-based clustering is a widely used technique within unsupervised learning algorithms in many research fields. The success of any centroid-based clustering relies on the choice of the similarity measure under use. In recent years, most studies focused on including several divergence measures in the traditional hard k-means algorithm. In this article, we consider the problem of centroid-based clustering using the family of α β -divergences, which is governed by two parameters, α and β . We propose a new iterative algorithm, α β -k-means, giving closed-form solutions for the computation of the sided centroids. The algorithm can be fine-tuned by means of this pair of values, yielding a wide range of the most frequently used divergences. Moreover, it is guaranteed to converge to local minima for a wide range of values of the pair ( α , β ). Our theoretical contribution has been validated by several experiments performed with synthetic and real data and exploring the ( α , β ) plane. The numerical results obtained confirm the quality of the algorithm and its suitability to be used in several practical applications.
Keywords: centroid-based clustering; k-means algorithm; musical genre clustering; unsupervised classification; αβ-divergence.
Conflict of interest statement
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Figures


References
-
- Amari S. α-Divergence Is Unique, Belonging to Both f-Divergence and Bregman Divergence Classes. IEEE Trans. Inf. Theory. 2009;55:4925–4931. doi: 10.1109/TIT.2009.2030485. - DOI
-
- Taneja I.J., Kumar P. Relative Information of Type s, CsiszáR’s F-divergence, and Information Inequalities. Inf. Sci. 2004;166:105–125. doi: 10.1016/j.ins.2003.11.002. - DOI
-
- Cichocki A., Amari S.i. Families of Alpha-Beta- and Gamma-Divergences: Flexible and Robust Measures of Similarities. Entropy. 2010;12:1532–1568. doi: 10.3390/e12061532. - DOI
-
- Banerjee A., Merugu S., Dhillon I.S., Ghosh J. Clustering with Bregman Divergences. J. Mach. Learn. Res. 2005;6:1705–1749.
-
- Nielsen F., Nock R. Sided and Symmetrized Bregman Centroids. IEEE Trans. Inf. Theory. 2009;55:2882–2904. doi: 10.1109/TIT.2009.2018176. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

