Informational Structures and Informational Fields as a Prototype for the Description of Postulates of the Integrated Information Theory
- PMID: 33267207
- PMCID: PMC7514983
- DOI: 10.3390/e21050493
Informational Structures and Informational Fields as a Prototype for the Description of Postulates of the Integrated Information Theory
Abstract
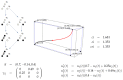
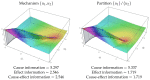
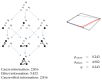
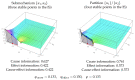
Informational Structures (IS) and Informational Fields (IF) have been recently introduced to deal with a continuous dynamical systems-based approach to Integrated Information Theory (IIT). IS and IF contain all the geometrical and topological constraints in the phase space. This allows one to characterize all the past and future dynamical scenarios for a system in any particular state. In this paper, we develop further steps in this direction, describing a proper continuous framework for an abstract formulation, which could serve as a prototype of the IIT postulates.
Keywords: Lotka–Volterra equations; dynamical system; global attractors; informational field; informational structure; integrated information theory.
Conflict of interest statement
The authors declare no conflict of interest. The funders had no role in the design of the study; the writing of the manuscript, or in the decision to publish the results.
Figures





Similar articles
-
Informational structures: A dynamical system approach for integrated information.PLoS Comput Biol. 2018 Sep 13;14(9):e1006154. doi: 10.1371/journal.pcbi.1006154. eCollection 2018 Sep. PLoS Comput Biol. 2018. PMID: 30212467 Free PMC article.
-
Integrated information and dimensionality in continuous attractor dynamics.Neurosci Conscious. 2017 May 30;2017(1):nix011. doi: 10.1093/nc/nix011. eCollection 2017. Neurosci Conscious. 2017. PMID: 30042844 Free PMC article.
-
New topological tool for multistable dynamical systems.Chaos. 2018 Nov;28(11):111101. doi: 10.1063/1.5062598. Chaos. 2018. PMID: 30501226
-
Integrated information theory of consciousness: an updated account.Arch Ital Biol. 2012 Jun-Sep;150(2-3):56-90. doi: 10.4449/aib.v149i5.1388. Arch Ital Biol. 2012. Corrected and republished in: Arch Ital Biol. 2012 Dec;150(4):293-329. PMID: 23165867 Corrected and republished. Review.
-
Dynamical systems, attractors, and neural circuits.F1000Res. 2016 May 24;5:F1000 Faculty Rev-992. doi: 10.12688/f1000research.7698.1. eCollection 2016. F1000Res. 2016. PMID: 27408709 Free PMC article. Review.
Cited by
-
Structural stability of invasion graphs for Lotka-Volterra systems.J Math Biol. 2024 Apr 17;88(6):64. doi: 10.1007/s00285-024-02087-8. J Math Biol. 2024. PMID: 38630280 Free PMC article.
-
Global structural stability and the role of cooperation in mutualistic systems.PLoS One. 2022 Apr 19;17(4):e0267404. doi: 10.1371/journal.pone.0267404. eCollection 2022. PLoS One. 2022. PMID: 35439272 Free PMC article.
-
What lies underneath: Precise classification of brain states using time-dependent topological structure of dynamics.PLoS Comput Biol. 2022 Sep 6;18(9):e1010412. doi: 10.1371/journal.pcbi.1010412. eCollection 2022 Sep. PLoS Comput Biol. 2022. PMID: 36067227 Free PMC article.
-
Integrated information theory (IIT) 4.0: Formulating the properties of phenomenal existence in physical terms.PLoS Comput Biol. 2023 Oct 17;19(10):e1011465. doi: 10.1371/journal.pcbi.1011465. eCollection 2023 Oct. PLoS Comput Biol. 2023. PMID: 37847724 Free PMC article.
-
Decrease and recovery of integrated information Φ during anesthesia and sleep on human functional magnetic resonance imaging.Neurosci Conscious. 2025 Sep 1;2025(1):niaf024. doi: 10.1093/nc/niaf024. eCollection 2025. Neurosci Conscious. 2025. PMID: 40901488 Free PMC article.
References
Grants and funding
- DEC-2017/25/B/ST1/00302/National Science Center (NCN) of Poland
- UMO-2016/22/A/ST1/00077/National Science Center (NCN) of Poland
- Proyecto de Excelencia FQM-1492/Consejería de Economía, Innovación, Ciencia y Empleo, Junta de Andalucía
- MTM2015-63723-P/Ministerio de Economía, Industria y Competitividad, Gobierno de España
LinkOut - more resources
Full Text Sources
Miscellaneous

