Magnetoconductivity in quasiperiodic graphene superlattices

Abstract

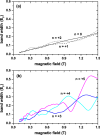
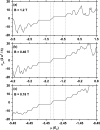
The magnetoconductivity in Fibonacci graphene superlattices is investigated in a perpendicular magnetic field B. It was shown that the B-dependence of the diffusive conductivity exhibits a complicated oscillatory behavior whose characteristics cannot be associated with Weiss oscillations, but rather with Shubnikov-de Haas ones. The absense of Weiss oscillations is attributed to the existence of two incommensurate periods in Fibonacci superlattices. It was also found that the quasiperiodicity of the structure leads to a renormalization of the Fermi velocity [Formula: see text] of graphene. Our calculations revealed that, for weak B, the dc Hall conductivity [Formula: see text] exhibits well defined and robust plateaux, where it takes the unexpected values [Formula: see text], indicating that the half-integer quantum Hall effect does not occur in the considered structure. It was finally shown that [Formula: see text] displays self-similarity for magnetic fields related by [Formula: see text] and [Formula: see text], where [Formula: see text] is the golden mean.

Figure 1

Diffusive conductivity (in units of ${\sigma }_0$) as a function of the applied magnetic field for several temperature values: (a) $T=4$ K, (b) $T=7$ K, and (c) $T=10$ K, where ${\sigma }_0=(e^2/h)(4\beta \tau E_F^2/ħ)$. Vertical dotted lines indicate the magnetic field intensities for which maxima have been obtained.

Figure 2

Center-position dependence and shifting $\beta (B)$ of the magnetic subbands corresponding to those magnetic fields at which the diffuse conductivity in Fig. 1 takes its maximum values. Note that the center of the $n=2,3,4$, and 5 magnetic subbands for $B=1.18$ T, 0.77 T, 0.58 T, and 0.46T, respectively, coincides with the $\mu =0$ chemical potential.

Figure 3

Magnetic field dependence of the band width for the $n=0$, $n=+1$, and $n=+2$ magnetic subbandas (a). In (b), the same results but for $n=+3$, $n=+4$, and $n=+5$.

Figure 4

Hall dc-conductivity (in units of $2e^2/h$) as a function of the chemical potential (in units of $E_C=ħ{\omega }_C$) for three values of the applied magnetic field, which are scaled by ${\tau }^2$ and ${\tau }^4$. The vertical lines determine the intervals for the plateaux that are around the $n=0$ shifted magnetic subbband.